Алгоритм RSA

Алгоритм rsa. программная реализация

Программа для шифрования алгоритмом RSA имеет интерфейс, представленный на рисунке 1.

В программе будем использовать следующий алфавит:

Число M(i) для конкретной буквы будет равно её номеру в массиве characters[].

Приведем код кнопки “Зашифровать”:

И кнопки “Расшифровать”:

Теперь покажем код остальных методов.

Проверка: является ли число простым?

Метод, выполняющий шифрование строки алгоритмом RSA описан ниже. Также вы можете узнать как изменились алгоритмы инстаграм в 2021:

При возведении числа в степень в данном случае получаются очень большие числа, которые не помещаются ни в один из стандартных типов. Поэтому для их хранения используется экземпляр класса BigInteger. Этот класс позволяет хранить целые числа произвольной (любой) длины и выполнять математические операции с ними.

Метод, выполняющий расшифровку строки алгоритмом RSA:

Вычисление параметра d (d должно быть взаимно простым с m).

Метод, вычисляющий значение параметра e.

Генерация ключей

Генерация ключей в схеме цифровой подписи RSА точно такая же, как и генерация ключей в криптографической системе RSА (см.

“B. Стандарты и организации по стандартизации”
). Алиса выбирает два простых числа p и q и вычисляет n = p x q. Алиса вычисляет e, для общедоступного ключа и вычисляет d для частного ключа, такое, что d и публично объявляет n и e.

В схеме цифровой подписи RSA. dявляется частным;. eи. n- общедоступными.

Подписание и проверка

Подписание. Алиса на основе сообщения создает подпись, используя частный (секретный) ключ, S = Md mod n, и передает сообщение и подпись Бобу.

Проверка. Боб получает М и S. Он применяет общедоступный ключ Алисы к подписи, чтобы создать копию сообщения М’ = Se mod n. Боб сравнивает значение М’ со значением М.

Последняя конгруэнтность справедлива, потому что “A. ASCII”).

Пример 3.1

Для безопасности подписи значения p и q должны быть очень большими. Как тривиальный пример, предположим, что Алиса выбирает p = 823 и q = 953 и вычисляет n = 784319. Значение 782544. Теперь она выбирает e = 313 и вычисляет d = 160009. В этой точке генерация ключей закончена. Теперь вообразим, что Алиса хочет передать сообщение со значением M = 19070 Бобу. Она использует свой частный ключ 160009 для того, чтобы подписать сообщение.

Атаки подписи RSA

Есть некоторые атаки, к которым Ева может обратиться для подделки схемы цифровой подписи RSА Алисы.

Атака только на ключ. Ева имеет доступ только к открытому ключу Алисы, перехватывает пару ( М, S ) и пробует создать другое сообщение М.’, такое, что М’ = Se mod n.

Эта проблема по сложности решения равна проблеме дискретного логарифма, которую мы рассмотрели в

“A. ASCII”
. Это – экзистенциальная подделка и обычно бесполезна для Евы.

Атака при известном сообщении. Здесь Ева использует мультипликативное свойство RSА. Предположим, что Ева перехватила две пары подписи сообщения – (M1, S1) и (M2, S2), которые используют один и тот же секретный ключ.

S = S1 x S2 mod n =
(M1d x M2d) mod n =
(M1 x M2)d mod n =
Md mod n

Ева может создать М. = M1 x M2 mod n и может создать S. = S1 x S2 mod n ; глупый Боб поверит, что S – подпись Алисы на сообщении М.

Эта атака, которая называется иногда мультипликативной атакой,
проводится очень просто. Однако это – экзистенциальная подделка так, как сообщение, М является произведением двух предыдущих сообщений, созданных Алисой, а не Евой; сообщение М. обычно бесполезно.

Атака по выбранному сообщению. Эта атака также использует мультипликативное свойство RSA. Ева может так или иначе попросить, чтобы Алиса подписала два законных сообщения М1 и М2.

С помощью их она позже создает новое сообщение М. = M1 x M2. Ева может позже утверждать, что Алиса подписала M. Такую атаку называют так же, как и предыдущую – мультипликативная атака.

Это очень серьезная атака схемы цифровой подписи RSA, потому что это – селективная подделка. (Ева может перемножать М1 и М2, чтобы получить полезный M ).

Подпись RSA на дайджесте сообщения

Как мы обсуждали прежде, подписание дайджеста сообщения и использование сильного алгоритма хэширования имеет несколько преимуществ. В случае RSA процессы подписания и проверки можно сделать намного быстрее, потому что схема цифровой подписи RSА – не что иное, как шифрование с секретным ключом и дешифрование с открытым ключом.

Алиса, подписывающее лицо, при первом использовании согласует
хэш-функцию, чтобы создать дайджест сообщенияD = h(M). Затем она подписывает дайджест, S = Dd mod n.

Сообщение и подпись передают Бобу. Боб, проверяющий, получает сообщение и подпись. Он сначала использует открытый ключ Алисы, чтобы извлечь (файл) дайджест, D’ = Se mod n. Затем он применяет хэш-алгоритм для того, чтобы получить сообщение D = h(M).

Боб теперь сравнивает эти два дайджеста, D и D’. Если они являются сравнимыми по модулю n, он принимает сообщение. Атаки на подписанные дайджесты RSA

Насколько восприимчива схема цифровой подписи RSA к нападению, когда дайджест уже подписан?

Атака только на ключ. Мы можем иметь три случая этой атаки.

1. Ева перехватывает пару (S, M) и пробует найти другое сообщение М’, которое создает тот же самый дайджест, h (M) = h (М’). Как мы узнали в

   “Целостность сообщения и установление подлинности сообщения”
   , если алгоритм хэшированияобладает устойчивостью ко второму прообразу,
   эта атака очень трудна.

2. Ева находит два сообщения, М. и М’, такие, что h(M) = h(M’). Она соблазняет Алису подписать h(M), чтобы найти S ; теперь Ева имеет пару (М’, S), которое прошло подтверждающий тест, но это – подделка. Мы изучали в

   “Целостность сообщения и установление подлинности сообщения”
   , что если алгоритм хэшированияустойчив к коллизиям, эта атака очень трудна.

3. Ева случайным подбором может найти дайджест сообщения D, который может соответствовать случайной подписи S. Она тогда находит сообщение М, такое, что D = h (M). Как мы узнали в

   “Целостность сообщения и установление подлинности сообщения”
   , если хэш-функция устойчива к прообразу, эта атака очень трудно осуществима.

Атака при известном сообщении. Предположим, что Ева имеет две пары подписи сообщения – (М1,S1) и (М2, S2), которые были созданы с использованием одного и того же секретного ключа.

Ева вычисляет S = S1 x S2. Если она сможет найти сообщение М, такое, что h(M) = h(M1) x h(M2), она сможет подделать новое сообщение.

Атаки по выбранному сообщению. Ева может попросить, чтобы Алиса подписала два законных сообщения – М1,и М2 для нее. Она может создать новую подпись S = S1 x S2.

Так как Ева может вычислить h(M) = h(M1) x h(M2), если она может найти сообщение M данному h (M), это новое сообщение – подделка. Однако нахождение М по данному h (M) -очень трудный процесс, если алгоритм хэшированияустойчив к прообразу.

Когда дайджест подписан непосредственно вместо сообщения, восприимчивость. схемы цифровой подписи RSAзависят от свойств алгоритма хэширования.

Стандарт цифровой подписи (dss)

Стандарт цифровой подписи (DSS – Digital Signature Standard) был принят национальным Институтом Стандартов и Технологии (NIST) в 1994 г. NIST издал DSS как FIPS-186 (FEDERAL INFORMATION PROCESSING STANDARD 186).

DSS применяет алгоритм цифровой подписи (DSA), основанный на схеме Эль-Гамаля, с использованием некоторых идей из схемы Шнорра. DSS критиковался со времени его издания.

В процессе подписания две функции создают две подписи; в процессе проверки выход одной функции сравнивается с первой подписью для проверки. Это подобно схеме Шнорра, но входы различны. Другое отличие: эта схема использует дайджест сообщения (не само сообщение) как часть входов к функциям 1 и 3.

Интересно то, что схема применяет два общедоступных модуля: p и q. Функции 1 и 3 используют оба модуля p и q, функция 2 – только q. Детали входов и функций коротко рассматриваются ниже.

Генерация ключей

Перед подписанием сообщения к любому объекту Алиса должна генерировать ключи и объявить общедоступные ключи.

1. Алиса выбирает простое число длиной p. между 512 и 1024 битами. Число битов в p должно быть кратно числу 64.
2. Алиса выбирает простое число на 160 битов q с таким условием, чтобы оно делилось на (p – 1).
3. Алиса использует две группы умножения, <Z_p*, x > и <Z_q* ,x > ; вторая – подгруппа первой.
4. Алиса создает e₁, такое, чтобы оно было q -тым корнем 1 по модулю p (e₁^p = 1 mod p). Она поступает так: выбирает элемент в Z_p, e₀, и вычисляет e₁ = e₀^(p-1)/q mod p.
5. Алиса выбирает d как секретный ключ и вычисляет e₂ = e₁^d
6. Общедоступный ключ Алисы – (e₁, e₂, p, q), ее секретный ключ – (d).

Подписание. Ниже показаны шаги подписания сообщения.

1. Алиса выбирает случайное число (1 <= r <= q). Обратите внимание, что хотя открытые и секретные ключи могут быть выбраны один раз и использоваться для того, чтобы подписать много сообщений, Алиса должна выбирать каждый раз новый r, когда она должна подписать новое сообщение.
2. Алиса вычисляет первую подпись S₁ = (e₁ mod p) mod q. Обратите внимание: значение первой подписи не зависит от М (сообщения).
3. Алиса создает дайджест сообщенияh (M).
4. Алиса вычисляет вторую подпись S₂ = (h(M) dS₁)r^-1mod q. Обратите внимание, что вычисление S₂ делается по модулю q.
5. Алиса посылает M, S₁ и S₂ Бобу.

Проверка (верификация). Для проверки сообщения обычно применяются следующие шаги, когда получены М, S1 и S2.

1. Боб проверяет S₁ 0 < S₁ < q.
2. Боб проверяет S₂ 0 < S₂ < q.
3. Боб вычисляет дайджест М, применяя алгоритм хэширования, используемый Алисой.
4. Боб вычисляет V = [(e₁^h(M)/S2 e₂^S1/S2) mod p] mod q.
5. Если S конгруэнтен V, сообщение принимается; иначе – отклоняется.

Пример 3.5

Алиса выбирает q = 101 и p = 8081. Алиса выбирает e0 = 3 и вычисляет e1 = e0(p-1)/q mod p = 6968.

Алиса выбирает d = 61 в качестве секретного ключа и вычисляет e2 = e1d mod p = 2038. Теперь Алиса может передать сообщение Бобу. Предположим, что h (M) = 5000, и Алиса выбирает r = 61:

Поскольку Sj и V являются подходящими, Боб принимает сообщение.

Сравнение DSS и RSА

Вычисление DSS-подписи быстрее, чем вычисление подписей RSА, при использовании того же самого p.

Сравнение DSS и схемы Эль-Гамаля

DSS-подпись – меньше, чем подписи в схеме Эль-Гамаля, потому что q меньше, чем p.

Схема цифровой подписи эллиптической кривой

Наша последняя схема – схема цифровой подписи эллиптической кривой(ECDSS – Elliptic Curve Digital Signature Scheme), которая основана на применении эллиптических кривых, – их мы обсуждали.

В процессе подписания две функции и экстрактор (извлекающее устройство) создают две подписи; в процессе проверки (верификации) обрабатывают выход одной функции (после прохождения через экстрактор) и сравнивают ее с первой подписью для проверки. Функции f1 и f3 фактически создают точки на кривой.

Первая создает новую точку для секретного ключа подписывающего лица. Вторая – новую точку из двух общедоступных ключей подписывающего лица. Каждый экстрактор извлекает первые координаты соответствующей точки в модульной арифметике. Детали входов и функций коротко обсуждаются далее.

Генерация ключей осуществляется следующими шагами:

1. Алиса выбирает эллиптическую кривуюEp (a,b) с
   простым числом p.
2. Алиса выбирает другое простое число q, чтобы использовать для вычисления.
3. Алиса выбирает секретный ключ d, целое число.
4. Алиса выбирает точку на кривой e₁(.,….)
5. Алиса вычисляет e₂ (..,….) = d x e₁ (……), другую точку на кривой.
6. Общедоступный ключ Алисы – (a, b, p, q, e₁, e₂), ее секретный ключ – d.

Подписание и проверка (верификация)

Подписание. Процесс подписания состоит главным образом из выбора секретного случайного числа, создания третьей точки на кривой, вычисления двух подписей и передачи сообщения и подписей.

1. Алиса выбирает секретное случайное число, r, между 1 и q – 1.
2. Алиса выбирает третью точку на кривой, P (U, v) = r x e₁ (……).
3. Алиса использует первые координаты P (u, v), чтобы вычислить первую подпись S_1. Это означает S₁ = u mod q.
4. Алиса использует дайджест сообщения, свой секретный ключ и секретное случайное число r и S₁, чтобы вычислить вторую подпись S₂ = (h (M) d x S₁) r^-1 mod q,
5. Алиса передает М, S₁ и S₂.

Проверка (верификация).Процесс проверки состоит главным образом из восстановления третьей точки и подтверждения, что первая координата эквивалентна S1 по модулю q. Обратите внимание, что третья точка была создана подписывающим лицом, использующим секретное случайное число r.

1. Боб применяет М, S₁ и S₂ для создания двух промежуточных результатов A и B:

   A = h(M)S₂^-1 mod q

   B = S₂^-1S₁ mod q

   Затем Боб восстанавливает третью точку T(x,y) = A x e₁( … , …) B x e₂( … , …)

2. Боб использует первую координату из T(x,y), чтобы проверить сообщение. Если x = S₁ mod q, подпись принимается, иначе – отклоняется.

Упражнения

1. Используя схему RSA, при p = 809, q = 751, и d = 23, вычислите общедоступный ключ e.

   Затем

2. Используя схему Эль-Гамаля при p = 881 и d = 700, найдите значения e₁ и e₂. Выберите r = 17. Найдите значение S₁ и S₂, если М = 400.
3. Используя схему Шнорра, при q = 83, p = 997 и d = 23, найдите значения для e₁ и e₂. Выберите r = 11. Если М
   = 400 и h (400) = 100, найдите значение S₁., S₂ и V. Равно ли ?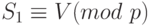
4. Используя схему DSS, при q = 59, p = 709 и d = 14, найдите значения для e₁ и e₂. Выберите r = 13. Найдите значение S₁ и S₂, если h (M) = 100. Проверьте подпись.
5. Сделайте следующее:
6. NIST-спецификация требует для DSS следующее: если значение S₂ = 0, то две подписи должны быть повторно вычислены, используя новый r. Какова причина этого?
7. Что случится, если Ева найдет значение r, используемое подписывающим лицом? Возможно ли это в принципе? Объясните ваш ответ отдельно для схем Эль-Гамаля-Шнорра, DSS.
8. Что случится, если Алиса подпишет два сообщения, используя одно и то же значение n? Объясните ваш ответ отдельно для каждого протокола: Эль-Гамаля, Шнорра или DSS.
9. Покажите пример уязвимости схемы RSA к селективной подделке, когда значения p и q являются маленькими. Используйте p = 19 и q = 3.
10. Покажите пример уязвимости схемы Эль-Гамаля к селективной подделке, когда значение p мало. Используйте p = 19.
11. Покажите пример уязвимости схемы Шнорра к селективной подделке, когда значения p и q являются маленькими. Используйте p =29 и q = 7.
12. Покажите пример уязвимости DSS к селективной подделке, когда значения p и q являются маленькими. Используйте p =29 и q = 7.
13. В схеме Эль-Гамаля, если Ева может найти значение r, может ли она подделать сообщение? Объясните.
14. В схеме Шнорра, если Ева может найти значение r, может ли она подделать сообщение? Объясните.
15. В DSS-схеме, если Ева может найти значение r, может ли она подделать сообщение? Объясните.
16. Предположим, что значения p, q, e₁ и r в схеме Шнорра – те же самые, что и соответствующие значения в DSS-схеме. Сравните значения S₁ и S₂ в схеме Шнорра с соответствующими значениями в DSS-схеме.
17. Объясните, почему в схеме Эль-Гамаля вычисление S₂ делается по модулю p, а вычисление S₂ делается по модулю p – 1.
18. Объясните, почему в схеме Шнорра вычисление S₁ делается по модулю p, а вычисление S₂ делается по модулю q.
19. Объясните, почему в схеме DSS вычисление S₁ делается по модулю p и модулю q, а вычисление S₂ делается только по модулю q.
20. В схеме Шнорра докажите правильность процесса проверки.
21. В DSS-схеме докажите правильность процесса проверки.
22. В схеме цифровой подписи эллиптической кривой докажите правильность процесса проверки.
23. Напишите два алгоритма для схемы RSА: один для процесса подписания и один для процесса проверки.
24. Напишите два алгоритма для схемы Эль-Гамаля: один для процесса подписания и один для процесса проверки.
25. Напишите два алгоритма для схемы Шнорра: один для процесса подписания и один для процесса проверки.
26. Напишите два алгоритма для DSS-схемы: один для процесса подписания и один для процесса проверки.
27. Напишите два алгоритма для схемы эллиптической кривой: один для процесса подписания и один для процесса проверки.