Алгоритмы быстрого возведения в степень — Википедия с видео // WIKI 2

Описание

Основным алгоритмом быстрого возведения в степень является схема «слева направо». Она получила своё название вследствие того, что биты показателя степени просматриваются слева направо, то есть от старшего к младшему[5].

Пусть

n=(mkmk−1…m1m0¯)2{displaystyle n=({overline {m_{k}m_{k-1}…m_{1}m_{0}}})_{2}} — двоичное представление степени n, то есть,

n=mk⋅2k mk−1⋅2k−1 ⋯ m1⋅2 m0,{displaystyle n=m_{k}cdot 2^{k} m_{k-1}cdot 2^{k-1} dots m_{1}cdot 2 m_{0},}

где mk=1,mi∈{0,1}{displaystyle m_{k}=1,m_{i}in {0,1}}. Тогда

xn=x((…((mk⋅2 mk−1)⋅2 mk−2)⋅2 …)⋅2 m1)⋅2 m0=((…(((xmk)2⋅xmk−1)2…)2⋅xm1)2⋅xm0{displaystyle x^{n}=x^{((dots ((m_{k}cdot 2 m_{k-1})cdot 2 m_{k-2})cdot 2 dots )cdot 2 m_{1})cdot 2 m_{0}}=((dots (((x^{m_{k}})^{2}cdot x^{m_{k-1}})^{2}dots )^{2}cdot x^{m_{1}})^{2}cdot x^{m_{0}}}^[5].

Последовательность действий при использовании данной схемы можно описать так:

1. Представить показатель степени n в двоичном виде
2. Если mi{displaystyle m_{i}} = 1, то текущий результат возводится в квадрат и затем умножается на x. Если mi{displaystyle m_{i}} = 0, то текущий результат просто возводится в квадрат^[6]. Индекс i изменяется от k-1 до 0^[7].

Таким образом, алгоритм быстрого возведения в степень сводится к мультипликативному аналогу схемы Горнера[6]:

{s1=xsi 1=si2⋅xmk−ii=1,2,…,k}.{displaystyle {begin{Bmatrix}s_{1}=x\s_{i 1}=s_{i}^{2}cdot x^{m_{k-i}}\i=1,2,dots ,kend{Bmatrix}}.}

Диафрагменное число

Если принять диаметр входного зрачка равным единице, геометрическое относительное отверстие может быть выражено следующим образом[4]:

N=Df′=1k{displaystyle N={D over f’}={1 over k}}.

В этом случае знаменатель относительного отверстия k{displaystyle k} называют диафрагменное число или «число диафрагмы». Диафрагменное число вычисляется как отношение фокусного расстояния объектива к диаметру его входного зрачка и обозначается цифрой.
Диафрагменное число является величиной, обратной относительному отверстию^[5][6].

k=f′D=1N{displaystyle k={f’ over D}={1 over N}}.

Этот параметр наиболее удобен для разметки шкал диафрагмы, поскольку не содержит дробей[7].
Регулировочная шкала ирисовой диафрагмы киносъёмочных объективов и фотообъективов старых типов (без автофокуса) градуируется в диафрагменных числах эффективного относительного отверстия, учитывающих потери света при его прохождении через стекло.

Каждое деление такой шкалы соответствует изменению светосилы в два раза, а относительного отверстия — в 2≈1,41{displaystyle {sqrt {2}}approx 1,41} раз^[7][2]. Исключение могут составлять самые малые значения диафрагменного числа, соответствующие оптическим возможностям объектива и не укладывающиеся в стандартный ряд^[8]. Такое строение шкалы диафрагменных чисел используется с 1950-х годов, когда появилось понятие экспозиционного числа, и позволяет при повороте кольца на одно деление менять экспозицию точно на одну экспозиционную ступень.

На современных фотообъективах такая шкала (как и кольцо регулировки диафрагмы) отсутствует, и установка диафрагмы производится дистанционно органами управления фотоаппарата. Шкала диафрагменных чисел современных цифровых фотоаппаратов имеет промежуточные значения, соответствующие 1/3 экспозиционной ступени:

При автоматическом управлении экспозицией относительное отверстие регулируется бесступенчато, поэтому диафрагменное число может принимать любые дробные значения.

Другие применения

Многие теоремы теории чисел допускают формулировку в терминах фигурных чисел. Например, гипотеза Каталана утверждает, что среди гиперкубических чисел произвольных размерностей только одна пара отличается на 1: 3 2 = 2 3 1 {displaystyle 3^{2}=2^{3} 1} (доказано в 2002 году).

Всякое чётное совершенное число является треугольным (и одновременно шестиугольным, причём номер шестиугольного числа есть степень двойки). Такое число не может одновременно быть квадратным, кубическим или иным гиперкубическим числом.

Гипотеза Лежандра (1808 год, она же третья проблема Эдмунда Ландау): между последовательными квадратными числами всегда найдётся простое число. До сих пор не доказана.

Сумма первых n {displaystyle n} центрированных треугольных чисел ( n > 2 ) {displaystyle (n>2)} есть «магическая константа» для магического квадрата размерности n × n {displaystyle n imes n} .

Другие способы получить эту же константу — через треугольное число T n 2 n , {displaystyle {frac {T_{n^{2}}}{n}},} или сложить все натуральные числа от T n − 1 {displaystyle T_{n-1}} до T n {displaystyle T_{n}} включительно.

Число Мерсенна, большее 1, не может быть квадратным, кубическим или иным гиперкубическим, но может быть треугольным. Треугольных чисел Мерсенна всего четыре: 1 , 3 , 5 , 4095 , {displaystyle 1,3,5,4095,} их поиск эквивалентен решению в натуральных числах уравнения Рамануджана — Нагеля: 2 n − 7 = x 2 . {displaystyle 2^{n}-7=x^{2}.

} Как оказалось, решение этого уравнения существует только при n = 3 , 4 , 5 , 7 , 15 {displaystyle n=3,4,5,7,15} (последовательность A060728 в OEIS), и при n >

3 {displaystyle n>3} соответствующее число Мерсенна M n − 3 {displaystyle M_{n-3}} будет тогда треугольным.

Число Ферма также не может быть квадратным, кубическим или иным гиперкубическим, но в единственном случае может быть треугольным: F 0 = 3. {displaystyle F_{0}=3.} Число Ферма также не может быть тетраэдральным и гипертетраэдральным любой размерности выше 2-й.

Среди чисел Фибоначчи имеются только три квадратных числа (0, 1 и 144) и четыре треугольных (1, 3, 21, 55, последовательность A039595 в OEIS). Если повернуть треугольник Паскаля, как показано на рисунке, то числа Фибоначчи можно получить как суммы вдоль восходящих диагоналей; этот факт даёт разложение числа Фибоначчи по гипертетраэдральным числам.

Среди чисел Люка квадратных чисел два (1 и 4), а треугольных три (1, 3, 5778).

Числа Каталана C a t n {displaystyle Cat_{n}} выражаются через гипертетраэдральные числа следующим образом:

C a t n = S n 1 [ n ] − S n 2 [ n − 1 ] {displaystyle Cat_{n}=S_{n 1}^{[n]}-S_{n 2}^{[n-1]}}

Ещё один класс чисел, тесно связанных с фигурными — числа Стирлинга второго рода S ( n , m ) . {displaystyle S(n,m).} Этот класс включает все треугольные числа: T n = S ( n 1 , n ) , {displaystyle T_{n}=S(n 1,n),} а выражение S ( n , 2 ) 1 {displaystyle S(n,2)

1} равно 2-му по порядку n {displaystyle n} -мерному гиперкубическому числу Q 2 [ n ] . {displaystyle Q_{2}^{[n]}.

} Наконец, всякое n {displaystyle n} -мерное гиперкубическое число разлагается по S ( n , m ) {displaystyle S(n,m)} следующим образом:

Q n [ d ] = ∑ m = 0 d S ( d , m ) x ( x − 1 ) … ( x − m 1 ) {displaystyle Q_{n}^{[d]}=sum _{m=0}^{d}{S(d,m)x(x-1)dots (x-m 1)}}

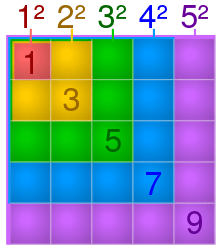
Квадратные числа

Квадратные числа представляют собой произведение двух одинаковых натуральных чисел, то есть являются полными квадратами:

1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900, 961, 1024, 1089, 1156, 1225, 1296, 1369, 1444, 1521, 1600, 1681, 1764, 1849, 1936, 2025, 2116, 2209, 2304, 2401, 2500 …, n 2 {displaystyle n^{2}} … (последовательность A000290 в OEIS)

Каждое квадратное число, кроме единицы, есть сумма двух последовательных треугольных чисел:

n 2 = T n − 1 T n {displaystyle n^{2}=T_{n-1} T_{n}} . Примеры: 4 = 1 3 ; 9 = 3 6 ; 16 = 6 10 {displaystyle 4=1 3;quad 9=3 6;quad 16=6 10} и т. д.

Сумма квадратов первых n {displaystyle n} натуральных чисел вычисляется по формуле:

1 2 2 2 3 2 . . . n 2 = n ( n 1 ) ( 2 n 1 ) 6 {displaystyle 1^{2} 2^{2} 3^{2} … n^{2}={frac {n(n 1)(2n 1)}{6}}}

Ряд обратных квадратов сходится:

∑ n = 1 ∞ 1 n 2 = 1 1 2 1 2 2 ⋯ 1 n 2 ⋯ = π 2 6 {displaystyle sum _{n=1}^{infty }{frac {1}{n^{2}}}={frac {1}{1^{2}}} {frac {1}{2^{2}}} dots {frac {1}{n^{2}}} dots ={frac {pi ^{2}}{6}}}

Каждое натуральное число может быть представлено как сумма не более четырёх квадратов (теорема Лагранжа о сумме четырёх квадратов).

Тождество Брахмагупты — Фибоначчи: произведение суммы двух квадратных чисел на любую другую сумму двух квадратных чисел само представимо в виде суммы двух квадратных чисел, причём двумя способами.

( a 2 b 2 ) ( c 2 d 2 ) = ( a c − b d ) 2 ( a d b c ) 2 = ( a c b d ) 2 ( a d − b c ) 2 . {displaystyle (a^{2} b^{2})(c^{2} d^{2})=(ac-bd)^{2} (ad bc)^{2}=(ac bd)^{2} (ad-bc)^{2}.}

Пример:

( 1 2 4 2 ) ( 2 2 7 2 ) = 26 2 15 2 = 30 2 1 2 . {displaystyle (1^{2} 4^{2})(2^{2} 7^{2})=26^{2} 15^{2}=30^{2} 1^{2}.}

Литература

• Шнайер Б.Алгоритмы с открытыми ключами // Прикладная криптография. — Триумф, 2002. — ISBN 5-89392-055-4.
• Рябко Б. Я., Фионов А. Н.Основы современной криптографии для специалистов в информационных технологиях — Научный мир, 2004. — С. 15. — 173 с. — ISBN 978-5-89176-233-6
• Смарт Н.Алгоритмы возведения в степень // Криптография. — Москва: Техносфера, 2005. — С. 287—292. — 528 с. — ISBN 5-94836-043-1.
• Маховенко Е. Б.Теоретико-числовые методы в криптографии — М.: Гелиос АРВ, 2006. — С. 154—155. — ISBN 978-5-85438-143-7
• Cohen H., Frei G. Handbook of Elliptic and Hyperelliptic Curve Cryptography. — Chapman & Hall/CRC, 2006. — С. 145—150. — 808 с. — ISBN 1-58488-518-1.
• Панкратова И. А.Теоретико-числовые методы криптографии — Томск: ТГУ, 2009. — 120 с.
• Габидулин Э. М., Кшевецкий А. С., Колыбельников А. И.Защита информации: учебное пособие — М.: МФТИ, 2021. — С. 230—231. — 225 с. — ISBN 978-5-7417-0377-9
• Крэндалл Р., Померанс К. Алгоритмы с открытыми ключами // Простые числа: Криптографические и вычислительные аспекты — М.: URSS, 2021. — С. 514—520. — 663 с. — ISBN 978-5-453-00016-6, 978-5-397-02060-2

Как только страница обновилась в Википедии она обновляется в Вики 2.Обычно почти сразу, изредка в течении часа.

Многоугольные числа, одновременно классические и центрированные

Некоторые центрированные многоугольные числа совпадают с классическими, например: 1 , 10 , 25 , 51 ; {displaystyle 1,10,25,51;} для краткости будем называть такие многоугольные числа двойными.

1. Двойные числа с общим параметром k {displaystyle k} (число углов): имеет место тождество: C k ( k ) = P k 1 ( k ) {displaystyle C_{k}^{(k)}=P_{k 1}^{(k)}quad } 2.

Двойные треугольные числа с разными k . {displaystyle k.} Пример: 1 , 10 , 136 , 1891 , 26335 … {displaystyle 1,10,136,1891,26335dots } (последовательность A128862 в OEIS).

Для их нахождения надо решить диофантово уравнение: m 2 m = 3 n 2 − 3 n 2 , {displaystyle m^{2} m=3n^{2}-3n 2,} тогда P m ( 3 ) = C n ( 3 ) . {displaystyle P_{m}^{(3)}=C_{n}^{(3)}.

} Некоторые решения: m = 1 , 4 , 16 , 61 , 229 … {displaystyle m=1,4,16,61,229dots } (последовательность A133161 в OEIS), соответственно: n = 1 , 3 , 10 , 36 , 133 … {displaystyle n=1,3,10,36,133dots } (последовательность A102871 в OEIS) 3.

Классические квадратные, являющиеся центрированными треугольными числами. Их определяет диофантово уравнение: m 2 = 3 n 2 − 3 n 2 2 . {displaystyle m^{2}={frac {3n^{2}-3n 2}{2}}.

quad } Тогда C m ( 3 ) = P n ( 4 ) . {displaystyle C_{m}^{(3)}=P_{n}^{(4)}.} Решения: m = 1 , 2 , 8 , 19 , 79 … {displaystyle m=1,2,8,19,79dots } (последовательность A129445 в OEIS), соответственно n = 1 , 2 , 7 , 16 , 65 … {displaystyle n=1,2,7,16,65dots } Первые такие числа: 1 , 4 , 64 , 361 , 6241 … {displaystyle 1,4,64,361,6241dots } 4.

Классические треугольные, являющиеся центрированными шестиугольными числами. Первые такие числа: 1 , 91 , 8911 , 873181 , 85562821 … {displaystyle 1,91,8911,873181,85562821dots } (последовательность A006244 в OEIS).

Их определяет диофантово уравнение: m ( m 1 ) 2 = 3 n 2 3 n 1. {displaystyle {frac {m(m 1)

}{2}}=3n^{2} 3n 1.quad } Тогда P m ( 3 ) = C n 1 ( 6 ) {displaystyle P_{m}^{(3)}=C_{n 1}^{(6)

}} Решения: m = 1 , 13 , 133 , 1321 , 13081 … {displaystyle m=1,13,133,1321,13081dots } (последовательность A031138 в OEIS) n = 0 , 5 , 54 , 539 , 5340 … {displaystyle n=0,5,54,539,5340dots } (последовательность A087125, в OEIS) 5.

Классические квадратные, являющиеся центрированными шестиугольными числами. Первые такие числа: 1 , 169 , 32761 , 6355441 , 1232922769 … {displaystyle 1,169,32761,6355441,1232922769dots } (последовательность A006051 в OEIS).

Их определяет диофантово уравнение: m 2 = 3 n 2 3 n 1. {displaystyle m^{2}=3n^{2} 3n 1.

quad } Тогда P m ( 4 ) = C n 1 ( 6 ) {displaystyle P_{m}^{(4)}=C_{n 1}^{(6)

}} Решения: m = 1 , 13 , 181 , 2521 , 35113 … {displaystyle m=1,13,181,2521,35113dots } (последовательность A001570 в OEIS) n = 0 , 7 , 104 , 1455 , 20272 … {displaystyle n=0,7,104,1455,20272dots } (последовательность A001921, в OEIS)

Определение, является ли заданное число многоугольным

Задача 1 (часто называемая задачей Диофанта): дано натуральное число N > 2 , {displaystyle N>2,} требуется определить, является ли оно многоугольным числом P n ( k ) {displaystyle P_{n}^{(k)}} и если да, то для каких значений k , n . {displaystyle k,n.

Тогда все соответствующие оставшимся парам P n ( k ) {displaystyle P_{n}^{(k)}} равны N . {displaystyle N.}

Пример. Пусть N = 105. {displaystyle N=105.} .

• Делители 2 N = 210 : 1 , 2 , 3 , 5 , 6 , 7 , 10 , 14 , 15 , 21 , 30 , 35 , 42 , 70 , 105 , 210. {displaystyle 2N=210colon quad 1,2,3,5,6,7,10,14,15,21,30,35,42,70,105,210.}
• Делители 2 N − 2 = 208 : 1 , 2 , 4 , 8 , 13 , 16 , 26 , 52 , 104 , 208. {displaystyle 2N-2=208colon quad 1,2,4,8,13,16,26,52,104,208.}
• Отбираем n = 2 , 3 , 5 , 14 , 105. {displaystyle n=2,3,5,14,105.}
• Соответственно k = 105 , 36 , 12 , 14 , 2. {displaystyle k=105,36,12,14,2.} Последнее значение отбросим.

Ответ: 105 {displaystyle 105} встречается как P 2 ( 105 ) , P 3 ( 36 ) , P 5 ( 12 ) , P 14 ( 14 ) , {displaystyle P_{2}^{(105)},P_{3}^{(36)},P_{5}^{(12)},P_{14}^{(14)},} то есть как 2-е 105-угольное, 3-е 36-угольное, 5-е 12-угольное и 14-е 14-угольное число.

Задача 2: дано натуральное число N > 2 , {displaystyle N>2,} требуется определить, является ли оно k-угольным числом P n ( k ) {displaystyle P_{n}^{(k)}} . В отличие от задачи 1, здесь k {displaystyle k} задано.

Для решения можно использовать тождество Диофанта:

8 ( k − 2 ) P n ( k ) ( k − 4 ) 2 = ( 2 n ( k − 2 ) − ( k − 4 ) ) 2 {displaystyle 8(k-2)P_{n}^{(k)} (k-4)^{2}=(2n(k-2)-(k-4))^{2}}

Это тождество без труда получается из приведенной выше общей формулы для P n ( k ) {displaystyle P_{n}^{(k)}} и равносильно ей.

Из тождества вытекает решение поставленной задачи 2: если N {displaystyle N} есть k-угольное число, то есть N = P n ( k ) {displaystyle N=P_{n}^{(k)}} для некоторого n , {displaystyle n,} то 8 ( k − 2 )

N ( k − 4 ) 2 {displaystyle 8(k-2)N (k-4)^{2}} есть некоторое квадратное число R 2 {displaystyle R^{2}} , и обратно. При этом номер n {displaystyle n} находится по формуле:

n = R k − 4 2 k − 4 {displaystyle n={frac {R k-4}{2k-4}}}

Пример. Определим, является ли число 1540 {displaystyle 1540} 10-угольным. Значение 8 ( k − 2 ) N ( k − 4 ) 2 {displaystyle 8(k-2)N (k-4)

^{2}} здесь равно 98596 = 314 2 , {displaystyle 98596=314^{2},} поэтому ответ утвердительный. n = 20 , {displaystyle n=20,} следовательно, 1540 {displaystyle 1540} является 20-м 10-угольным числом.

Оптимизация алгоритма

Как правило, операция возведения в квадрат выполняется быстрее операции умножения. Метод окон позволяет сократить количество операций умножения и, следовательно, сделать алгоритм возведения в степень более оптимальным[8].

Окно фактически представляет собой основание системы счисления[7]. Пусть w — ширина окна, то есть за один раз учитывается w знаков показателя.

Рассмотрим метод окна.

1. Для i=0,2w−1¯{displaystyle i={overline {0,2^{w}-1}}} заранее вычисляется xⁱ
2. Показатель степени представляется в следующем виде: n=∑i=0k/wni⋅2i⋅w{displaystyle n=sum _{i=0}^{k/w}{n_{i}cdot 2^{icdot w}}}, где ni∈(0,1,…,2w−1){displaystyle n_{i}in {(0,1,…,2^{w}-1)}}
3. Пусть y — переменная, в которой будет вычислен конечный результат. Положим y=xnk/w{displaystyle y=x^{n_{k/w}}}.
4. Для всех i = k/w — 1, k/w — 2, …, 0 выполнить следующие действия:
   1. y=y2w{displaystyle y=y^{2^{w}}}
   2. y=y⋅xni{displaystyle y=ycdot x^{n_{i}}}^[8].

В данном алгоритме требуется k возведений в квадрат, но число умножений в среднем сокращается до k/w[8].

Ещё более эффективным является метод скользящего окна. Он заключается в том, что ширина окна во время выполнения процесса может изменяться:

1. Показатель степени представляется в виде n=∑i=0lni⋅2ei{displaystyle n=sum _{i=0}^{l}{n_{i}cdot 2^{e_{i}}}}, где ni∈(1,3,5,…,2w−1){displaystyle n_{i}in {(1,3,5,…,2^{w}-1)}}, а e_{i 1} — e_i ≥ w.
2. Для i=(1,3,5,…,2w−1){displaystyle i=(1,3,5,…,2^{w}-1)} вычисляется xⁱ. Далее будем обозначать xⁱ как x_i.
3. Пусть y — переменная, в которой будет вычислен конечный результат. Положим y=xnl{displaystyle y=x^{n_{l}}}.
4. Для всех i = l — 1, l — 2, …, 0 выполнить следующие действия:
   1. Для всех j от 0 до e_{i 1} — e_i — 1 y возвести в квадрат
   2. j=mi{displaystyle j=m_{i}}
   3. y=y⋅xj{displaystyle y=ycdot x_{j}}
5. Для всех j от 0 до e₀ — 1 y возвести в квадрат^[8].

Количество операций возведения в степень в данном алгоритме такое же, как и в методе окна, а вот количество операций умножений сократилось до l, то есть до kw 1{displaystyle {frac {k}{w 1}}} в среднем^[8].

Для примера возведём методом скользящего окна число x в степень 215. Ширина окна w = 3.

1. 215 = 2⁷ 5 · 2⁴ 7
2. y = 1
3. y = y · x = x
4. y 3 раза возводится в квадрат, так как на данном шаге e₂ — e₁ −1 = 7 — 4 — 1 = 2, а отсчёт ведётся с нуля, то есть y = y⁸ = x⁸
5. y = y · x⁵ = x¹³
6. y 4 раза возводится в квадрат, так как на данном шаге e₁ — e₀ −1 = 4 — 0 — 1 = 3, то есть y = y¹⁶= x²⁰⁸
7. y = y · x⁷ = x²¹⁵

Приложение для анизокинетического отбора проб частиц

Например, селективный захват частиц центрированным тонкостенным круглым соплом описывается Беляевым и Левиным как:

c/c0знак равно1 (ты0/ты-1)(1-11 Sтk(2 0,617ты/ты0)){ displaystyle c / c_ {0} = 1 (u_ {0} / u-1) left (1 – { frac {1} {1 mathrm {Stk} (2 0,617u / u_ {0 })}}правильно)}

где – концентрация частиц, – скорость, а нижний индекс 0 указывает условия далеко перед соплом. Характерное расстояние – это диаметр сопла. Здесь вычисляется число Стокса,
c{ displaystyle c}ты{ displaystyle u}

Sтkзнак равноты0Vsdг{ displaystyle mathrm {Stk} = { frac {u_ {0} V_ {s}} {dg}}}

где – скорость оседания частицы, – внутренний диаметр пробоотборных трубок, – ускорение свободного падения.
Vs{ displaystyle V_ {s}}d{ displaystyle d}г{ displaystyle g}

Примеры решения задач

Применяя алгоритм, вычислим 2113:

1310=11012{displaystyle 13_{10}=1101_{2}}

m3=1,m2=1,m1=0,m0=1{displaystyle m_{3}=1,m_{2}=1,m_{1}=0,m_{0}=1}

2113=(((1⋅21m3)2⋅21m2)2⋅21m1)2⋅21m0=(((1⋅211)2⋅211)2⋅210)2⋅211=(((1⋅21)2⋅21)2⋅1)2⋅21=((212⋅21)2)2⋅21=((441⋅21)2)2⋅21=857661212⋅21=154472377739119461{displaystyle {begin{aligned}21^{13}&=(((1cdot 21^{m_{3}})^{2}cdot 21^{m_{2}})^{2}cdot 21^{m_{1}})^{2}cdot 21^{m_{0}}\&=(((1cdot 21^{1})^{2}cdot 21^{1})^{2}cdot 21^{0})^{2}cdot 21^{1}\&=(((1cdot 21)^{2}cdot 21)^{2}cdot 1)^{2}cdot 21\&=((21^{2}cdot 21)^{2})^{2}cdot 21\&=((441cdot 21)^{2})^{2}cdot 21\&=85766121^{2}cdot 21\&=154472377739119461end{aligned}}}

Примечания

Производящая функция

Степенной ряд, коэффициенты которого — k-угольные числа, сходится при | x | < 1 {displaystyle |x|<1} :

P 1 ( k ) x P 2 ( k ) x 2 P 3 ( k ) x 3 ⋯ = x ( 1 ( k − 3 ) x ) ( 1 − x ) 3 {displaystyle P_{1}^{(k)}x P_{2}^{(k)}x^{2} P_{3}^{(k)}x^{3} dots ={frac {x(1 (k-3)x)}{(1-x)^{3}}}}

Выражение справа является производящей функцией для последовательности k-угольных чисел.

Аппарат производящих функций позволяет применять в теории чисел и комбинаторике методы математического анализа. Приведенная формула также объясняет появление k-угольных чисел среди коэффициентов ряда Тэйлора для различных рациональных дробей. Примеры:

При k = 3 {displaystyle k=3} : x ( 1 − x ) 3 = P 1 ( 3 ) x P 2 ( 3 ) 3 x 2 P 3 ( 3 ) x 3 ⋯ P n ( 3 ) x n … {displaystyle qquad {frac {x}{(1-x)

^{3}}}=P_{1}^{(3)}x P_{2}^{(3)}3x^{2} P_{3}^{(3)}x^{3} dots P_{n}^{(3)}x^{n} dots } При k = 4 {displaystyle k=4} : x ( x 1 ) ( 1 − x ) 3 = P 1 ( 4 ) x P 2 ( 4 ) 3 x 2 P 3 ( 4 ) x 3 ⋯ P n ( 4 ) x n … {displaystyle qquad {frac {x(x 1)}{(1-x)

^{3}}}=P_{1}^{(4)}x P_{2}^{(4)}3x^{2} P_{3}^{(4)}x^{3} dots P_{n}^{(4)}x^{n} dots } При k = 5 {displaystyle k=5} : x ( 2 x 1 ) ( 1 − x ) 3 = P 1 ( 5 ) x P 2 ( 5 ) 3 x 2 P 3 ( 5 ) x 3 ⋯ P n ( 5 ) x n … {displaystyle qquad {frac {x(2x 1)}{(1-x)^{3}}}=P_{1}^{(5)}x P_{2}^{(5)}3x^{2} P_{3}^{(5)}x^{3} dots P_{n}^{(5)}x^{n} dots }

и т. д.

Для некоторых классов многоугольных чисел существуют свои, специфические производящие функции. Например, для квадратных треугольных чисел 1 , 36 , 1225 , 41616 , 1413721 … {displaystyle 1,36,1225,41616,1413721dots } производящая функция имеет следующий вид:

x ( 1 x ) ( 1 − x ) ( 1 − 34 x x 2 ) = x 36 x 2 1225 x 3 … {displaystyle {frac {x(1 x)}{(1-x)(1-34x x^{2})

}}=x 36x^{2} 1225x^{3} dots } ; ряд сходится при | x | < 17 − 12 2 {displaystyle |x|<17-12{sqrt {2}}}

Расчёт относительного отверстия

Геометрическое относительное отверстие N{displaystyle N} выражают в виде дроби^[2]:

N=Df′{displaystyle N={D over f’}},

где D{displaystyle D} обозначает диаметр входного зрачка, а f′{displaystyle f’} — заднее фокусное расстояние. Относительное отверстие принято обозначать соотношением двух чисел, написанных через двоеточие. При этом первое число всегда принимается за единицу, например 1:5,6. В современной литературе более широкое распространение получило обозначение относительного отверстия в виде дроби с числителем f, например f/5,6. Для зеркально-линзовых объективов площадь входного зрачка рассчитывается по более сложному закону, поскольку его центральная часть экранирована^[1]. В этом случае диафрагма может иметь форму не круга, а кольца, и для нахождения диаметра входного зрачка необходимо реальный входной зрачок (кольцо) заменить при расчёте кругом эквивалентной площади. Диаметр найденного круга и будет являться искомым диаметром входного зрачка для применения в дальнейших расчётах.
Квадрат относительного отверстия называется светосилой и определяет соотношение яркости объекта и освещённости его изображения в фокальной плоскости^[1].
Эффективное относительное отверстие вычисляется с учётом коэффициента светопропусканияτ{displaystyle tau } оптической системы, учитывающего общую толщину стекла и количество границ воздух/стекло.
Коэффициент, снижающий прозрачность объектива, определяется по формуле:

τ=(1−P)n⋅(1−α)m{displaystyle tau =(1-P)^{n}cdot (1-alpha )^{m}},

где P{displaystyle P} — доля света, теряемая при отражении одной поверхностью раздела сред;

n{displaystyle n} — число поверхностей раздела воздух/стекло;

α{displaystyle alpha } — удельное поглощение света в 1 сантиметре стекла;

m{displaystyle m} — суммарная толщина линз объектива в сантиметрах.

Для объективов без просветления τ{displaystyle tau } не превышает 0,65. Объективы с просветлением теряют не более 10% света при его прохождении и рассеянии.

Приведённые способы расчёта геометрического и эффективного относительного отверстия справедливы только при фокусировке объектива на «бесконечность». Для конечных дистанций знаменатель дроби увеличивается из-за выдвижения объектива, приводя к уменьшению относительного отверстия.

Эффект особенно заметен при макросъёмке, когда сопряжённое фокусное расстояние может превосходить расчётное в два и более раз. В этом случае пренебрегать изменением относительного отверстия недопустимо и требуются поправки при расчёте экспозиции[3].

Рекомендации

Схема «справа налево»

В данной схеме, в отличие от схемы «слева направо», биты показателя степени просматриваются от младшего к старшему[5].

Последовательность действий при реализации данного алгоритма.

1. Представить показатель степени n в двоичном виде.
2. Положить вспомогательную переменную z равной числу x.
   1. Если mi=1{displaystyle m_{i}=1}, то текущий результат умножается на z, а само число z возводится в квадрат. Если mi{displaystyle m_{i}} = 0, то требуется только возвести z в квадрат^[6]. При этом индекс i, в отличие от схемы слева направо, изменяется от 0 до k-1 включительно^[7].

Данная схема содержит столько же умножений и возведений в квадрат, сколько и схема «слева направо». Однако несмотря на это, схема «слева направо» выгоднее схемы «справа налево», особенно в случае, если показатель степени содержит много единиц. Дело в том, что в схеме слева направо в операции result = result · x содержится постоянный множитель x.

А для небольших x (что нередко бывает в тестах простоты) умножение будет быстрым. К примеру, для x = 2 мы можем операцию умножения заменить операцией сложения[7].

Математическое обоснование работы данного алгоритма можно представить следующей формулой:

d=an={displaystyle d=a^{n}=}

=a∑i=0kmi⋅2i={displaystyle =a^{sum _{i=0}^{k}m_{i}cdot 2^{i}}=}

=am0⋅a2m1⋅a22∗m2⋅…⋅a2k∗mk={displaystyle =a^{m_{0}}cdot a^{2m_{1}}cdot a^{2^{2}*m_{2}}cdot …cdot a^{2^{k}*m_{k}}=}

=am0⋅(a2)m1⋅(a22)m2⋅…⋅(a2k)mk={displaystyle =a^{m_{0}}cdot (a^{2})^{m_{1}}cdot (a^{2^{2}})^{m_{2}}cdot …cdot (a^{2^{k}})^{m_{k}}=}

=∏i=0k(a2i)mi{displaystyle =prod _{i=0}^{k}{(a^{2^{i}})^{m_{i}}}}^[9].

Пример. Посчитаем с помощью схемы возведения в степень «справа налево» значение 2113.

1. 21 · 194 481 = 4084 101
2. 4084 101 · 37 822 859 361 = 154 472 377 739 119 461