- Что такое электронная подпись
- Основа эп — асимметричное шифрование
- 1 Хэш-функции
- 2.1 Общие положения
- 2.2 Схема Эль-Гамаля
- 2.3 Скрытый канал
- 2.4 Цифровая подпись на эллиптических кривых
- Второй учебный алгоритм хеширования
- Генерация подписи
- Как работает: алгоритмы шифрования
- Как работает: сертификаты
- Некоторые наиболее употребительные схемы эцп
- Первый учебный алгоритм хеширования
- Пример генерации подписи
- Принцип работы электронной подписи
- Проверка подписи
- Список литературы
- Хеш-функции
- Электронная цифровая подпись для чайников: с чем ее есть и как не подавиться. часть 3
Что такое электронная подпись
Электронная подпись — это технология, которая помогает подтвердить подлинность электронного документа: договора, справки, выписки или чего-то ещё.
Если упрощённо, работает так:
👉 Есть некий документ, подписанный ЭП
👉 С помощью специальной программы можно проверить подлинность этой подписи и документа
✅ Если программа говорит, что всё окей, то мы можем быть уверены: документ подписал именно тот, кто в нём указан; и с момента подписания в документе ничего не изменилось.
❌ Или программа может сказать, что подпись не совпала. Это значит, что либо документ подписал другой человек, либо после подписания кто-то изменил этот документ (например, дописал ноль в стоимость контракта). Так мы поймём, что этому документу нельзя доверять.
Электронная подпись нужна, чтобы защищать договоры, выдавать официальные справки, заключать сделки и участвовать в торгах по госзакупкам.
Основа эп — асимметричное шифрование
Мы уже писали об асимметричном шифровании. Вот основные мысли:
- В симметричном алгоритме зашифровать и расшифровать сообщение можно только одним и тем же ключом. Это полезно для передачи секретных сообщений, когда две стороны доверяют друг другу и могут заранее обменяться ключом.
- При асимметричном сообщение шифруется одним ключом, а расшифровывается другим. В разных комбинациях этот алгоритм помогает шифровать сообщения, когда стороны друг другу не доверяют или не могут обменяться ключами заранее. В частности, это полезно для подтверждения подлинности документов.
1 Хэш-функции
Определение 9.1Хэш-функции – это функции, предназначенные для “сжатия” произвольного сообщения, записанного, как правило, в двоичном алфавите, в некоторую битовую последовательность фиксированной длины, называемую сверткой.
Хэш-функции применяются для тестирования логических устройств, для быстрого поиска и проверки целостности записей в базах данных.
В криптографии хэш-функции применяются для решения следующих задач:
При решении первой задачи для каждого набора данных вычисляется значение хеш-функции (называемое кодом аутентификации сообщения или имитовставкой), которое передается или хранится вместе с самими данными.
При получении данных пользователь вычисляет значение свертки и сравнивает его с имеющимся контрольным значением. Несовпадение говорит о том, что данные были изменены. При решении второй задачи, аутентификации источника данных, мы имеем дело с не доверяющими друг другу сторонами.
В связи с этим подход, при котором обе стороны обладают одним и тем же секретным ключом, уже не применим. В такой ситуации применяют схемы цифровой подписи, позволяющие осуществить аутентификацию источника данных. Как правило, при этом сообщение, прежде чем быть подписано личной подписью, основанной на секретном ключе пользователя, “сжимается” с помощью хеш-функции, выполняющей функцию кода обнаружения ошибок.
Определение 9.2Обозначим через  множество, элементы которого будем называть сообщениями,
множество, элементы которого будем называть сообщениями,  – натуральное число. Хеш-функцией называется всякая легко вычислимая функция
– натуральное число. Хеш-функцией называется всякая легко вычислимая функция 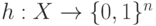 .
.
Кроме того, хэш-функцию можно понимать, как отображение из множества сообщений в некоторое ограниченное подмножество целых неотрицательных чисел.
Обычно число возможных сообщений значительно превосходит число возможных значений сверток, в силу чего для каждого значения свертки имеется большое множество прообразов, то есть сообщений с заданным значением хеш-функции. Заметим, что при случайном и равновероятном выборе сообщений условие равномерности распределения значений хеш-функции эквивалентно наличию одинакового числа прообразов для каждого значения свертки.
Как правило, хеш-функции строят на основе так называемых одношаговых сжимающихся функций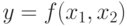




 длина свертки. Для получения значения
длина свертки. Для получения значения 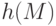

 длина сообщения не кратна
длина сообщения не кратна 
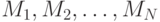
 вектор. Если функция
вектор. Если функция вектор можно положить равным нулевому вектору. Если же функция
вектор можно положить равным нулевому вектору. Если же функция вектор можно составить из фрагментов указывающих на дату, время, номер сообщения и т.п.При таком подходе свойства хеш-функции
вектор можно составить из фрагментов указывающих на дату, время, номер сообщения и т.п.При таком подходе свойства хеш-функции 

2.1 Общие положения
Появление криптографии с открытым ключом позволило решать задачи, которые ранее считались неразрешимыми. К таким задачам относится использование цифрового аналога собственноручной подписи абонента – электронной цифровой подписи (ЭЦП).
Цифровая подпись (ЭЦП) для сообщения является числом, зависящим от самого сообщения и от секретного ключа, известного только подписывающему. Важное требование: подпись должна допускать проверку без знания секретного ключа. При возникновении спорной ситуации, связанной с отказом от факта подписи либо с возможной подделкой подписи, третья сторона должна иметь возможность разрешить спор.
Задачи, которые решает подпись:
Для реализации схемы ЭЦП необходимы два алгоритма: алгоритм генерации подписи и алгоритм проверки. Надежность схемы ЭЦП определяется сложностью следующих задач:
Заметим, что между ЭЦП и собственноручной подписью имеются различия, хотя они и служат для решения одинаковых задач. Так, ЭЦП зависит от подписываемого текста, различна для разных тестов. Кроме того, ЭЦП требует дополнительных механизмов, реализующих алгоритмы ее вычисления и проверки.
Наконец, принципиальной сложностью, возникающей при использовании ЭЦП, является необходимость создания инфраструктуры открытых ключей. Эта инфраструктура состоит из центров сертификации открытых ключей и обеспечивает возможность своевременного подтверждения достоверности открытой информации, необходимой для проверки ЭЦП, что необходимо для предотвращения подделки подписи.
2.2 Схема Эль-Гамаля
См. [1]
Безопасность схемы основана на трудности вычисления дискретных логарифмов в конечном поле. Для генерации пары ключей выбирается простое число 



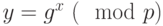
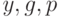






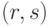
Для проверки подписи нужно убедиться, что
Первое замечание о выборе 






Схема Эль-Гамаля послужила образцом для построения большого семейства во многом сходных по своим свойствам схем подписи.
Пример 9.1Выберем 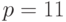 и
и  , а секретный ключ
, а секретный ключ 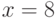 .
.
Вычислим:
Открытым ключом являются 

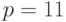
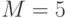


Теперь находим
Итак, подпись представляет собой пару: 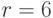

Для проверки подписи убедимся, что:
Второе замечание. При вычислении подписи целесообразно использовать хэш-образ сообщения, а не само сообщение 
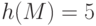 хеширования и шифрования с открытым ключом (в частности, RSA или Эль-Гамаля).
хеширования и шифрования с открытым ключом (в частности, RSA или Эль-Гамаля).
Алгоритм формирования подписи выглядит следующим образом:
Пусть
 – подписываемое сообщение. Отправитель вычисляет хеш-значение подписываемого сообщения
– подписываемое сообщение. Отправитель вычисляет хеш-значение подписываемого сообщения 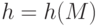 . Значение
. Значение  должно удовлетворять неравенству
должно удовлетворять неравенству 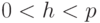 .
.- Отправитель выбирает случайное число
 ,
, 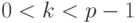 , взаимно простое с
, взаимно простое с  , и вычисляет числа:
, и вычисляет числа: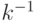 – число, обратное
– число, обратное  по модулю
по модулю  ,
, 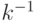 существует, так как
существует, так как  и
и  – взаимно просты.
– взаимно просты. - Подпись
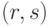 добавляется к сообщению, и тройка
добавляется к сообщению, и тройка 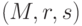 передается получателю.
передается получателю.
Проверка подписи: получатель заново вычисляет хеш-значение присланного сообщения 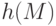
Если подпись верна, то это равенство выполняется.
Отметим, что число 
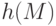
2.3 Скрытый канал
См. [2]
Иногда требуется иметь дополнительную возможность организации скрытого канала связи в открытых сообщениях, хотя сообщения сами по себе не содержат секретной информации. В этом случаи используют скрытый канал, иногда называемый также подсознательным каналом.
Густовус Симпсон придумал идею организации подсознательного канала с помощью обычного алгоритма цифровой подписи. Так как подсознательные сообщения спрятаны в том, что выглядит нормальными цифровыми подписями, это форма маскировки. Проверяющий видит, как подписанные безобидные сообщения передаются между отправителем и получателем, но реальная передаваемая информация проходит незаметно для него по подсознательному каналу.
В действительности, алгоритм подсознательного канала в подписях не отличим от нормального алгоритма в подписях. Проверяющий не только не может прочитать сообщение, передаваемое по подсознательному каналу, но у него вообще нет ни малейшего представления о существовании такового сообщения.
В общем случае организация подсознательного канала выглядит так:
- Отправитель создает безобидное сообщение;
- Используя общий ключ с получателем сообщения, отправитель подписывает безобидное сообщение, пряча свое подсознательное сообщение в подписи;
- Отправитель посылает подписанное сообщение по общедоступному каналу передачи;
- Проверяющий читает сообщение и проверяет подпись. Не обнаружив ничего подозрительного, он передает сообщение дальше;
- Получатель проверяет подпись под безобидным сообщением, убеждаясь что сообщение получено от отправителя;
- Получатель игнорирует безобидное сообщение и, используя общий с отправителем секретный ключ, извлекает подсознательное сообщение;
Рассмотрим простейший пример организации подсознательного канала передачи информации используя цифровую подпись реализуемую по методу Эль-Гамаля.
Сначала необходимо сгенерировать пару ключей, для этого выбирается простое
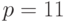 и два случайных
и два случайных  и
и 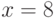 , причем
, причем 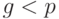 и
и 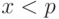 . Затем вычисляется
. Затем вычисляется 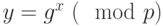 ,
,  . Открытым ключом является
. Открытым ключом является  , секретным ключом
, секретным ключом 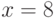 ;
;Создают безобидное сообщение
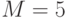 и скрытое сообщение
и скрытое сообщение 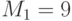 , проверяя чтобы эти сообщения были взаимно простые с
, проверяя чтобы эти сообщения были взаимно простые с  , а также чтобы
, а также чтобы  было взаимно простым c
было взаимно простым c  ; В нашем случае это так;
; В нашем случае это так;- Вычисляем значение цифровой подписи
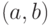
Мы получили подпись
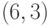 и в тоже время создали скрытый канал;
и в тоже время создали скрытый канал; - Проверяющий может просмотреть безобидное сообщение и удостовериться что сообщение передано от отправителя с подписью
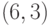 , для этого он проводит вычисления:
, для этого он проводит вычисления: - Получатель, обладающий секретным ключом, удостоверяется в том, что сообщение пришло именно от того отправителя, с которым организован скрытый канал, для этого он проводит вычисления:
- Получатель восстанавливает скрытое сообщение:
2.4 Цифровая подпись на эллиптических кривых
См. [3]
В качестве международного стандарта принят американский алгоритм цифровой подписи на эллиптических кривых (ECDSA). В этом стандарте используются эллиптические кривые как над полем простого порядка, так и над полем характеристики 2. Однако криптографически стойких кривых над полем характеристики 2 сравнительно мало. Поэтому мы рассмотрим ЭЦП на эллиптических кривых, заданных над полем большей характеристики.
Замечание. В России официально принят стандарт ЭЦП на эллиптических кривых над полем большей характеристики – ГОСТ 34.10-2001 “Информационная технология. Криптографическая защита информации. Процессы формирования и проверки электронной цифровой подписи”. Выбор кривой и точки на ней подразумевает решение ряда вспомогательных задач. Прежде всего, это подсчет количества точек на кривой. Если 






Для получения криптографически стойкой системы ЭЦП должны выполняться следующие условия:
- Порядок точки
 , используемой в системе ЭЦП, должен быть простым числом
, используемой в системе ЭЦП, должен быть простым числом 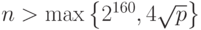 .
. 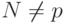 и
и 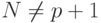 , где
, где  – порядок кривой.
– порядок кривой. для всех
для всех  , где
, где  настолько велико, что вычислить дискретный логарифм в
настолько велико, что вычислить дискретный логарифм в  за приемлемое время невозможно.
за приемлемое время невозможно.
Замечание. В настоящее время значение 







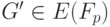
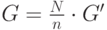


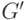

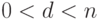
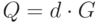

Второй учебный алгоритм хеширования
В этом алгоритме 

Начальное значение
 принимается равным числу десятичных разрядов в
принимается равным числу десятичных разрядов в  .
.- Для каждого десятичного знака
 числа
числа  вычисляется значение
вычисляется значение - Значение
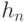 , вычисленное для последнего символа, увеличенное на 1, является хеш-значением сообщения:
, вычисленное для последнего символа, увеличенное на 1, является хеш-значением сообщения:  .
.
Вычисленное по этому алгоритму хеш-значение зависит от всех символов сообщения  Пример 9.3Известны значения общих параметров системы Эль-Гамаля:
Пример 9.3Известны значения общих параметров системы Эль-Гамаля: 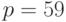 ,
, 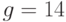 и открытый ключ абонента
и открытый ключ абонента 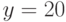 . От абонента получено сообщение
. От абонента получено сообщение 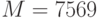 , снабженное цифровой подписью Эль-Гамаля
, снабженное цифровой подписью Эль-Гамаля 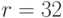 ,
, 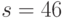 . Проверить подлинность цифровой подписи. Хеш-значение сообщение вычисляется с помощью второго учебного алгоритма.
. Проверить подлинность цифровой подписи. Хеш-значение сообщение вычисляется с помощью второго учебного алгоритма.
Вычисляем значения
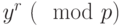 и
и  , а затем их произведение по модулю
, а затем их произведение по модулю  :
:В рассматриваемом примере получаем:
- Для полученного сообщения вычисляем хеш-значение
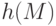 по второму учебному алгоритму.
по второму учебному алгоритму. - Вычисляем значение
 .
.В примере
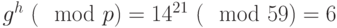 .
. - Проверяем выполнение равенства
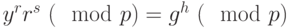 , если равенство выполняется – подпись подлинная, в противном случае – фальшивая.
, если равенство выполняется – подпись подлинная, в противном случае – фальшивая.В нашем примере
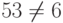 . Равенство не выполняется, значит, подпись фальшивая.
. Равенство не выполняется, значит, подпись фальшивая.
Генерация подписи
Входные данные: сообщение 
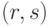
Алгоритм:
Выбрать случайное число 
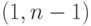
- Вычислить
 .
. - Вычислить
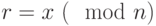 .
. - Если
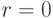 , то вернуться к шагу 1.
, то вернуться к шагу 1. - Вычислить
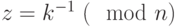 .
. - Вычислить
 .
. - Вычислить
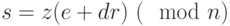 .
. - Если
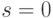 , то вернуться к шагу 1.
, то вернуться к шагу 1. - Вывести пару
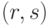 – подпись к
– подпись к  .
.
Замечания.
- При
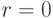 результат вычисления
результат вычисления  не зависит от секретного ключа
не зависит от секретного ключа  .
. - При
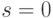 необходимого для проверки подписи числа
необходимого для проверки подписи числа  не существует.
не существует. - В качестве хеш-функции
 на 6 в стандартах ANSI X9F1 и IEEE P1363 используется SHA-1, в российском стандарте ГОСТ Р 34.10-2001~- хеширование по стандарту ГОСТ Р 34.11-94.
на 6 в стандартах ANSI X9F1 и IEEE P1363 используется SHA-1, в российском стандарте ГОСТ Р 34.10-2001~- хеширование по стандарту ГОСТ Р 34.11-94.
Как работает: алгоритмы шифрования
Допустим, вы уже сходили в удостоверяющий центр и получили на флешке сертификат и ключ электронной подписи. Теперь нужно скачать специальный софт, который и будет подписывать ваши документы и проверять чужие на подлинность.
Проблема в том, что ЭП основана на алгоритмах асимметричного шифрования, а их много: разложение на простые множители, дискретное логарифмирование, эллиптические кривые и множество других. Ключ из одного алгоритма не подойдёт для использования в другом, поэтому в России договорились использовать стандарт шифрования ГОСТ Р 34.
Это значит, что нам нужен специальный софт, в котором уже есть этот алгоритм. Чаще всего используют КриптоПРО, реже — ViPNet CSP. С помощью этих программ можно подписать документы и проверить сертификаты на подлинность.
Как работает: сертификаты
Электронная подпись состоит из двух принципиальных частей:
- Сертификат для удостоверения подписывающего.
- Криптографическая часть для проверки подлинности документа.
Грубо говоря, ЭП должна гарантировать, что документ подписали именно вы и что вы подписали именно этот документ.
В сертификате хранятся данные о владельце подписи:
- кто владелец этой подписи;
- открытый ключ для проверки подписи;
- когда заканчивается срок действия подписи;
- какого уровня документы можно подписывать этой подписью;
- кто выдал сертификат;
- и другие служебные данные.
Но смысл сертификата не в том, что там хранятся эти данные, а в том, кто эти данные туда положил. В России сертификаты и ЭП выдают специальные удостоверяющие центры — это компании, которые гарантируют, что сертификат выдаётся именно тому, кто в этом сертификате указан.
Чтобы получить сертификат, вы приходите лично в эту компанию (удостоверяющий центр), показываете документы, фотографируетесь. Вас заносят в базу удостоверяющего центра и выдают ключи электронной подписи. Так все участники электронного документооборота будут уверены, что все документы, подписанные вашими ключами, подписаны именно вами.
Некоторые наиболее употребительные схемы эцп
В настоящее время имеется большое количество различных схем ЭЦП, обеспечивающих тот или иной уровень стойкости. Существующие схемы можно классифицировать таким образом:
Первый учебный алгоритм хеширования
Входом для данного алгоритма является строка, состоящая из букв русского языка.
Выбирается число
 – вектор инициализации. Число
– вектор инициализации. Число  равно длине сообщения в символах.
равно длине сообщения в символах.Для каждого символа сообщения вычисляется значение
 , где
, где 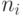 – номер
– номер  -й буквы сообщения в алфавите. Для удобства вычислений ниже приведен нумерованный алфавит.
-й буквы сообщения в алфавите. Для удобства вычислений ниже приведен нумерованный алфавит.- Значение
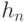 , вычисленное для последнего символа, является хеш-значением сообщения:
, вычисленное для последнего символа, является хеш-значением сообщения: 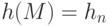 .
.
Следует отметить, что вычисленное по этому алгоритму хеш-значение зависит от всех символов сообщения 
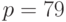
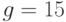


 Пример 9.2Выполнить вычисление и проверку подписи сообщения
Пример 9.2Выполнить вычисление и проверку подписи сообщения  по алгоритму Эль-Гамаля. Использовать параметры подписи:
по алгоритму Эль-Гамаля. Использовать параметры подписи:
- Сформируем хэш-сумму сообщения. Начальное значение
 равно количеству символов сообщения:
равно количеству символов сообщения:  . Далее,
. Далее, - Вычисляем число
 по формуле
по формуле 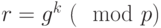 . Для рассматриваемого примера получили:
. Для рассматриваемого примера получили: - Вычисляем число
 по формуле
по формуле  , для рассматриваемого примера
, для рассматриваемого примера - Вычисляем значение
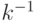 по модулю
по модулю  с помощью расширенного алгоритма Евклида. Для рассматриваемого примера значение
с помощью расширенного алгоритма Евклида. Для рассматриваемого примера значение  .
.Примечание: если полученное значение
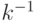 – отрицательное, следует взять его по модулю
– отрицательное, следует взять его по модулю  .
. - Вычисляем число
 по формуле
по формуле 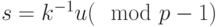 . В примере
. В примере - Цифровая подпись сообщения для рассматриваемого примера:
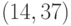 .
.
Для проверки правильности вычисления полученной цифровой подписи следует произвести ее проверку с помощью открытого ключа абонента и убедиться, что подпись подлинная.
- Сформируем открытый ключ
 абонента по формуле
абонента по формуле 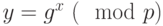 :
:Для рассматриваемого примера
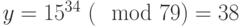 .
. Аналогичным образом вычисляем значения
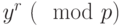 и
и  , а затем их произведение по модулю
, а затем их произведение по модулю  .
.В примере получаем:
- Вычисляем значение
 , значение
, значение  было получено ранее.
было получено ранее.В примере
 .
. - Проверяем выполнение равенства
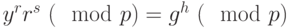 , если равенство выполняется – подпись подлинная, то есть она была вычислена правильно.
, если равенство выполняется – подпись подлинная, то есть она была вычислена правильно.В примере получили
 , равенство выполняется, значит, подпись сгенерирована правильно.
, равенство выполняется, значит, подпись сгенерирована правильно.
Пример генерации подписи
Наша цель – показать особенности алгоритма, не зависящие от разрядности чисел.
Пример 9.4Пусть используется эллиптическая кривая  и генерирующая точка
и генерирующая точка  порядка
порядка 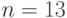 (13 – наибольший из делителей порядка кривой
(13 – наибольший из делителей порядка кривой 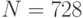 ). Предположим, абонент подписывает личным секретным ключом
). Предположим, абонент подписывает личным секретным ключом 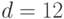 сообщение, хеш-свертка которого равна
сообщение, хеш-свертка которого равна 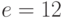 . Сгенерировать подпись.Пусть абонент, подписывающий сообщение, выбрал случайное
. Сгенерировать подпись.Пусть абонент, подписывающий сообщение, выбрал случайное 



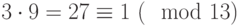


В реально использующихся системах ЭЦП по российскому стандарту числа имеют порядка 60 десятичных знаков.
Принцип работы электронной подписи
Электронная подпись работает по ассиметричному принципу шифрования. То есть документ зашифровывается с помощью закрытого ключа, а расшифровывается с помощью открытого.
Подписание документа производится в несколько этапов:
- Хеш документа шифруется с помощью закрытого ключа.
- Полученная подпись добавляется к документу.
- К документу прикрепляется сертификат проверки.
Проверка подписи
Входные данные: сообщение 

Выходные данные: заключение о подлинности или фальсификации подписи.
Алгоритм:
- Если хотя бы одно из условий
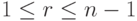 ,
,  нарушается, то подпись фальшивая и работа алгоритма закончена.
нарушается, то подпись фальшивая и работа алгоритма закончена. - Вычислить
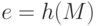 .
. - Вычислить
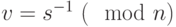 .
. - Вычислить
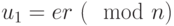 .
. - Вычислить
 .
. - Вычислить
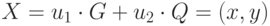 .
. - Если
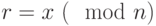 , то подпись действительная, иначе подпись фальшивая.
, то подпись действительная, иначе подпись фальшивая.
Доказательство корректности алгоритма генерации и алгоритма проверки подписи очень простое и предоставляется в качестве упражнения.
Пример 9.5Требуется проверить подлинность подписи (11,9) для сообщения  , хэш-образ которого
, хэш-образ которого 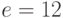 .Секретный ключ нам неизвестен, открытый ключ абонента, подписавшего сообщение, равен
.Секретный ключ нам неизвестен, открытый ключ абонента, подписавшего сообщение, равен 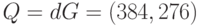 .Проверка подписи начинается с проверки условий
.Проверка подписи начинается с проверки условий 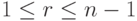
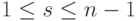
Находим точку
Наконец, сравниваем значения 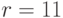

Приведем пример системы электронной подписи на эллиптической кривой, пригодный для практического применения.
Пример 9.6Рассмотрим эллиптическую кривую
Её порядок
является простым числом, а порождающим элементом группы является точка
Для построения электронной подписи нужно выбрать закрытый ключ 
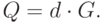
Система цифровой подписи построена.
Если читатель не имеет инструмента для работы с кривыми таких размеров, предлагаем небольшую программу на языке с , вызывающую функцию библиотеки cryptopp для перемножение точек:
Для её сборки нужно подключить библиотеку cryptopp (см. параграф 1.16.2). Допустим, мы собрали программу в исполняемый файл mulpoint (или mulpoint.exe под Windows).
Программа запускается из командной строки:
и выводит результат через стандартный выходной поток. Например:
(здесь $ – приглашение командной строки linux). В нашем случае, помимо 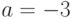
Список литературы
- Васильева И.Н. Защита информации — СПб, 2009. — 136 с.
- Шнайер Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си — М.: Триумф, 2003. — 816 с.
- Харин Ю.С., Берник В.И., Матвеев Г.В. Математические основы криптологии — Минск: БГУ, 1999. — 319 с.
- Жданов О.Н., Чалкин В.А. Эллиптические кривые. Основы теории и криптографические приложения — М.: УРСС, 2021.
- Schoof, R. Counting points on elliptic curves over finite fields //J. de Th'{e}orie des Nombres de Bordeaux. — textnumero 7 (1995). — p. 219-254.
- Lercier, R., Morain, F. Counting the number of points on elliptic curves over finite fields: strategies and performances,
- In L. C. Guillou and J.-J. Quisquater, editors, Advances in cryptology — EUROCRYPT’95, textnumero 921 (1995) of Lecture Notes in Comput. Sci. p. 79-94.
- NIST FIPS 186-4, July 2021.
Хеш-функции
Хеширование — это процесс преобразования массива входных данных произвольной длины в (выходную) битовую строку фиксированной длины. Например, хеш-функция может принимать строку с любым количеством знаков (одна буква или целое литературное произведение), а на выходе получать строку со строго определенным числом символов (дайджест).
Хеш-функции имеются практически в любом языке программирования. Например, они используются для реализации хеш-таблиц и множеств (HashMap/HashSet в Java, dict и set в Python, Map, Set и объекты в JavaScript и так далее). Отдельная категория хеш-функций — криптографические хеш-функции.
К ним предъявляются существенно более строгие требования, чем к функциям, обычно используемым в хеш-таблицах. Поэтому и применяются они в более «серьезных» случаях, например для хранения паролей. Криптографические хеш-функции вырабатываются и тщательно проверяются исследователями по всему миру.
Поэкспериментировать с хеш-функциями можно, написав простую программу на Python:
import hashlib
def hash_hex(message):
return hashlib.sha256(message.encode()).hexdigest()
Функция hash_hex() рассчитывает представление хеша в шестнадцатеричной записи для строки. В приведенном примере используется функция SHA-256 — та же, что и в биткойне.
Хорошая хеш-функция обеспечивает защиту от коллизий (невозможно получить два одинаковых хеша при разных начальных данных) и обладает так называемым эффектом лавины, когда малейшее изменение входных данных значительно преобразует выходное значение. Эффект лавины в хеш-функции SHA-256 выглядит следующим образом:
Электронная цифровая подпись для чайников: с чем ее есть и как не подавиться. часть 3
Часть 2
В этой части сделаем небольшое отступление от цифровых подписей в сторону того, без чего непосредственно цифровых подписей, да и защиты информации в привычном понимании, не было бы: шифрования. Ведь первое, что приходит на ум, когда идет речь о защите наших данных — это не дать эти данные нехорошему человеку прочитать. Поэтому, перед тем, как продолжить рассмотрение стандартов PGP и S/MIME, стоит закрасить некоторые остающиеся в знаниях белые пятна, и рассмотреть процесс шифрования немного поподробнее.
Шифры и коды существуют, наверное, с того момента, как человечество научилось записывать свои впечатления об окружающем мире на носителях. Если немного вдуматься, даже обыкновенный алфавит — уже шифр. Ведь когда мы читаем какой-либо текст, в нашей голове каждому нарисованному символу сопоставляется некий звук, сочетание звуков, или даже целое понятие, а в голове соседа, который читать не умеет, этого уже не происходит.
Не зная, какому символу и что сопоставлено, мы никогда не сможем понять, что же именно писавший имел ввиду. К примеру, попробуйте взять и прочитать что-то, написанное на иврите, или на китайском языке. Сами алфавиты этих языков будут являться для вас непреодолимым препятствием, даже если с помощью этих символов написаны понятия вашего родного языка.
Но, тем не менее, простое использование чужого алфавита все же недостаточная мера для защиты ваших данных. Ведь любой алфавит, так или иначе, создавался для удобства пользования им и является неразрывно связанным с языком, которому данный алфавит характерен. А значит, выучив этот язык и некоторый набор базовых понятий на нем (а то и просто воспользовавшись услугами человека, знающего данный язык), нехороший человек может прочитать вашу информацию.
Значит, надо придумать алфавит, который знает только ограниченный круг лиц, и с его помощью записать информацию. Наверняка все читали (или, по крайней мере, слышали) цикл историй про Шерлока Холмса. В этом цикле фигурировал алфавит, составленный из пляшущих человечков (а многие, я думаю, в детстве на его основе составляли свой). Однако, как показывает данная история, наблюдательный человек может разгадать, какой символ и к чему относится. А значит наша информация опять попадет не в те руки.
Что же делать? Придумывать все более и более сложные алфавиты? Но чем более сложный и громоздкий алфавит, тем более неудобно с ним работать, хранить его в тайне. К тому же, насчет тайны есть замечательная поговорка: знают двое – знают все. Ведь самое слабое звено в любом шифре – это человек, который знает, как этот шифр расшифровать.
А почему бы не сделать так, чтобы способ шифрования был сразу известен всем, но расшифровать наши данные было бы нельзя без какого-то ключа? Ведь ключ (в отличие от всего алфавита) маленький, его достаточно легко сделать новый, если что (опять же, в отличие от переработки всего алфавита), легко спрятать. Наиболее наглядно плюсы ключевых систем показывает следующий пример: получателю надо прочитать сосланное вами сообщение. Обычное, на бумаге. Допустим, вы используете секретный алфавит. Тогда, чтобы прочитать сообщение, получатель должен знать алфавит, иметь большой пыльный талмуд, в котором описаны способы расшифровки (ведь алфавит должен быть сложным, чтобы быть надежным) и понимать, как же с этим талмудом работать. С ключами же все проще: вы кладете сообщение в коробку с замком, а получателю достаточно просто вставить подходящий ключик, а знать, как же устроен замок ему совершенно но нужно.
Итак, общеизвестные «алфавиты» и ключи — механизм, существенно более удобный, чем просто алфавиты. Но как же так зашифровать, чтобы все расшифровывалось простым ключом? И вот тут нам на помощь приходит математика, а конкретнее – математические функции, которые можно использовать для замены наших исходных символов на новые.
Вспомним же, что такое функция. Это некоторое соотношение, по которому из одного числа можно получить другое. Зная x и подставляя его в известное нам соотношение y=A*x, мы всегда получим значение y. Но ведь, как правило, верно и обратное: зная y, мы можем получить и x.
Как правило, но далеко не всегда. Для многих зависимостей получить y легко, тогда как x – уже очень трудно, и его получение займет продолжительное время. Вот именно на таких зависимостях и базируется используемое сейчас шифрование.
Но, вернемся к самому шифрованию. Шифрование подразделяют на симметричное, асимметричное и комбинированное. Рассмотрим, в чем суть каждого из них.
Симметричное шифрование, по большому счету, достаточно слабо отличается от старого доброго секретного алфавита. Собственно говоря, отличается оно как раз наличием ключа – некоторой сравнительно маленькой последовательности чисел, которая используется для шифрования и расшифровывания. При этом, каждая из обменивающихся информацией сторон должна этот ключ знать и хранить в секрете. Огромным плюсом такого подхода является скорость шифрования: ключ, по сути, является достаточно простой и короткой инструкцией, какой символ, когда, и на какой надо заменять. И работает данный ключ в обе стороны (то есть с его помощью можно как заменить все символы на новые, так и вернуть все как было), за что такой способ шифрования и получил название симметричного. Столь же огромным минусом является именно то, что обе стороны, между которыми информация пересылается, должны ключ знать. При этом, стоит нехорошему человеку заполучить ключ, как он тут же прочитает наши столь бережно защищаемые данные, а значит проблема передачи ключа принимающей стороне становится в полный рост.
Асимметричное шифрование поступает несколько хитрее. Здесь и у нас, и у нашего получателя есть уже два ключа, которые называют открытый и закрытый. Закрытый ключ мы и получатель храним у себя (заметьте, каждый хранит только свой ключ, а значит, мы уже выходим за пределы той самой поговорки про двоих знающих), а открытый мы и получатель можем спокойно передавать кому угодно – наш закрытый, секретный, по нему восстановить нельзя. Итого, мы используем открытый ключ получателя для шифрования, а получатель, в свою очередь, использует свой закрытый ключ для расшифровывания. Плюс данного подхода очевиден: мы легко можем начать обмениваться секретной информацией с разными получателями, практически ничем (принимая условие, что наш получатель свой закрытый ключ не потерял/отдал и т.п., то есть не передал его в руки нехорошего человека) не рискуем при передаче информации. Но, без огромного минуса не обойтись. И здесь он в следующем: шифрование и расшифровывание в данном случае идут очень, очень, очень медленно, на два-три порядка медленнее, чем аналогичные операции при симметричном шифровании. Кроме того, ресурсов на это шифрование тратится также значительно больше. Да и сами ключи для данных операций существенно длиннее аналогичных для операций симметричного шифрования, так как требуется максимально обезопасить закрытый ключ от подбора по открытому. А значит, большие объемы информации данным способом шифровать просто невыгодно.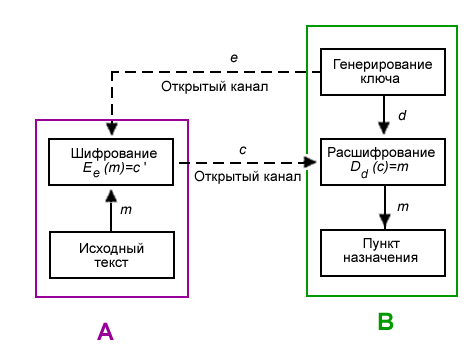
Пример использования асимметричного шифрования [Wikipedia]
e — открытый ключ получателя B
d — закрытый ключ получателя B
m — исходная информация отправителя A
c — зашифрованная исходная информация
И снова возникает вопрос: что же делать? А делать нужно следующее: взять, и скомбинировать оба способа. Собственно, так мы и получаем комбинированное шифрование. Наш большой объем данных мы зашифруем по первому способу, а чтобы донести ключ, с помощью которого мы их зашифровали, до получателя, мы сам ключ зашифруем по второму способу. Тогда и получим, что хоть асимметричное шифрование и медленное, но объем зашифрованных данных (то есть ключа, на котором зашифрованы большие данные) будет маленьким, а значит расшифровывание пройдет достаточно быстро, и дальше уже в дело вступит более быстрое симметричное шифрование.
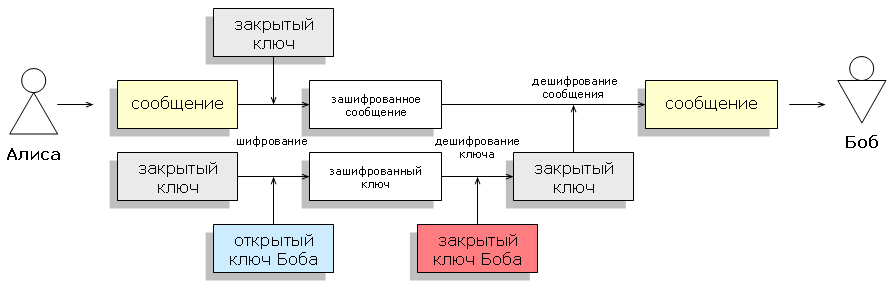
Пример применения комбинированной системы [Wikipedia]
Все эти механизмы нашли свое применение на практике, и оба наших больших лагеря PGP и S/MIME их используют. Как говорилось в первой статье, асимметричное шифрование используется для цифровой подписи (а именно, для шифрования нашего хэша). Отличие данного применения от обычного асимметричного шифрования в том, что для шифрования используется наш закрытый ключ, а для расшифровывания достаточно наличие связанного с ним (то есть, тоже нашего) открытого ключа. Поскольку открытый ключ мы не прячем, наш хэш можем прочитать кто угодно, а не только отдельный получатель, что и требуется для цифровой подписи.
Комбинированное же шифрование применяется в обоих стандартах непосредственно для шифрования отправляемых данных.
Таким образом, начиная пользоваться цифровыми подписями для защиты наших данных от подмены, мы автоматически (для этих двух стандартов) получаем и замечательную возможность защитить наши данные еще и от прочтения, что, согласитесь, весьма удобно.
Теперь, когда мы познакомились с общими принципами работы механизмов, используемых для защиты наших данных, можно наконец перейти к практике и рассмотрению, что же использовать. Но об этом в следующих статьях.




