- 2.1 Общие положения
- 2.2 Схема Эль-Гамаля
- Keccak
- Второй учебный алгоритм хеширования
- Как появилось понятие хэш?
- Квалифицированная электронная подпись
- Криптографические хэш-функции в помощь it-юристу
- Общие сведения
- Первый учебный алгоритм хеширования
- Практическое применение
- Принцип работы эцп
- Простая электронная подпись
- Стандарты хеширования: популярные варианты
- Функция перестановок
- Электронная подпись для чайников: с чем ее есть и как не подавиться. часть 2
2.1 Общие положения
Появление криптографии с открытым ключом позволило решать задачи, которые ранее считались неразрешимыми. К таким задачам относится использование цифрового аналога собственноручной подписи абонента – электронной цифровой подписи (ЭЦП).
Цифровая подпись (ЭЦП) для сообщения является числом, зависящим от самого сообщения и от секретного ключа, известного только подписывающему. Важное требование: подпись должна допускать проверку без знания секретного ключа. При возникновении спорной ситуации, связанной с отказом от факта подписи либо с возможной подделкой подписи, третья сторона должна иметь возможность разрешить спор.
Задачи, которые решает подпись:
Для реализации схемы ЭЦП необходимы два алгоритма: алгоритм генерации подписи и алгоритм проверки. Надежность схемы ЭЦП определяется сложностью следующих задач:
Заметим, что между ЭЦП и собственноручной подписью имеются различия, хотя они и служат для решения одинаковых задач. Так, ЭЦП зависит от подписываемого текста, различна для разных тестов. Кроме того, ЭЦП требует дополнительных механизмов, реализующих алгоритмы ее вычисления и проверки.
Наконец, принципиальной сложностью, возникающей при использовании ЭЦП, является необходимость создания инфраструктуры открытых ключей. Эта инфраструктура состоит из центров сертификации открытых ключей и обеспечивает возможность своевременного подтверждения достоверности открытой информации, необходимой для проверки ЭЦП, что необходимо для предотвращения подделки подписи.
2.2 Схема Эль-Гамаля
См. [1]
Безопасность схемы основана на трудности вычисления дискретных логарифмов в конечном поле. Для генерации пары ключей выбирается простое число 



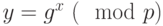
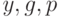






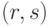
Для проверки подписи нужно убедиться, что
Первое замечание о выборе 






Схема Эль-Гамаля послужила образцом для построения большого семейства во многом сходных по своим свойствам схем подписи.
Пример 9.1Выберем 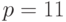 и
и  , а секретный ключ
, а секретный ключ 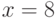 .
.
Вычислим:
Открытым ключом являются 

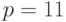
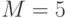


Теперь находим
Итак, подпись представляет собой пару: 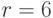

Для проверки подписи убедимся, что:
Второе замечание. При вычислении подписи целесообразно использовать хэш-образ сообщения, а не само сообщение 
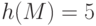 хеширования и шифрования с открытым ключом (в частности, RSA или Эль-Гамаля).
хеширования и шифрования с открытым ключом (в частности, RSA или Эль-Гамаля).
Алгоритм формирования подписи выглядит следующим образом:
Пусть
 – подписываемое сообщение. Отправитель вычисляет хеш-значение подписываемого сообщения
– подписываемое сообщение. Отправитель вычисляет хеш-значение подписываемого сообщения 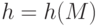 . Значение
. Значение  должно удовлетворять неравенству
должно удовлетворять неравенству 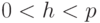 .
.- Отправитель выбирает случайное число
 ,
, 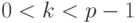 , взаимно простое с
, взаимно простое с  , и вычисляет числа:
, и вычисляет числа: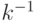 – число, обратное
– число, обратное  по модулю
по модулю  ,
, 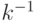 существует, так как
существует, так как  и
и  – взаимно просты.
– взаимно просты. - Подпись
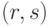 добавляется к сообщению, и тройка
добавляется к сообщению, и тройка 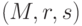 передается получателю.
передается получателю.
Проверка подписи: получатель заново вычисляет хеш-значение присланного сообщения 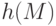
Если подпись верна, то это равенство выполняется.
Отметим, что число 
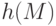
Keccak
Хеш-функции семейства Keccak построены на основе конструкции криптографической губки, в которой данные сначала «впитываются» в губку, а затем результат Z «отжимается» из губки.
Любая губчатая функция Keccak использует одну из семи перестановок Keccak-f[1600], для неё количество раундов
Давайте сразу введем понятие строки состояния, которая играет важную роль в алгоритме.
Строка состояния представляет собой строку длины 1600 бит, которая делится на
Алгоритм получения хеш-функции можно разделить на несколько этапов:
• С помощью функции дополнения исходное сообщение M дополняется до строки P длины кратной r
• Строка P делится на n блоков длины
Все сразу станет понятно, когда вы посмотрите на картинку ниже:
Функция дополнения
В SHA-3 используется следующий шаблон дополнения 10…1: к сообщению добавляется 1, после него от 0 до r – 1 нулевых бит и в конце добавляется 1.
r – 1 нулевых бит может быть добавлено, когда последний блок сообщения имеет длину r – 1 бит. В этом случае последний блок дополняется единицей и к нему добавляется блок, состоящий из r – 1 нулевых бит и единицы в конце.
Если длина исходного сообщения M делится на r, то в этом случае к сообщению добавляется блок, начинающийся и оканчивающийся единицами, между которыми находятся r – 2 нулевых бит. Это делается для того, чтобы для сообщения, оканчивающегося последовательностью бит как в функции дополнения, и для сообщения без этих бит значения хеш-функции были различны.
Первый единичный бит в функции дополнения нужен, чтобы результаты хеш-функции от сообщений, отличающихся несколькими нулевыми битами в конце, были различны.
Второй учебный алгоритм хеширования
В этом алгоритме 

Начальное значение
 принимается равным числу десятичных разрядов в
принимается равным числу десятичных разрядов в  .
.- Для каждого десятичного знака
 числа
числа  вычисляется значение
вычисляется значение - Значение
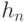 , вычисленное для последнего символа, увеличенное на 1, является хеш-значением сообщения:
, вычисленное для последнего символа, увеличенное на 1, является хеш-значением сообщения:  .
.
Вычисленное по этому алгоритму хеш-значение зависит от всех символов сообщения  Пример 9.3Известны значения общих параметров системы Эль-Гамаля:
Пример 9.3Известны значения общих параметров системы Эль-Гамаля: 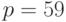 ,
, 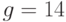 и открытый ключ абонента
и открытый ключ абонента 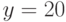 . От абонента получено сообщение
. От абонента получено сообщение 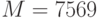 , снабженное цифровой подписью Эль-Гамаля
, снабженное цифровой подписью Эль-Гамаля 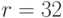 ,
, 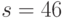 . Проверить подлинность цифровой подписи. Хеш-значение сообщение вычисляется с помощью второго учебного алгоритма.
. Проверить подлинность цифровой подписи. Хеш-значение сообщение вычисляется с помощью второго учебного алгоритма.
Вычисляем значения
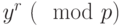 и
и  , а затем их произведение по модулю
, а затем их произведение по модулю  :
:В рассматриваемом примере получаем:
- Для полученного сообщения вычисляем хеш-значение
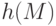 по второму учебному алгоритму.
по второму учебному алгоритму. - Вычисляем значение
 .
.В примере
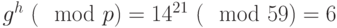 .
. - Проверяем выполнение равенства
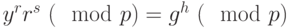 , если равенство выполняется – подпись подлинная, в противном случае – фальшивая.
, если равенство выполняется – подпись подлинная, в противном случае – фальшивая.В нашем примере
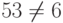 . Равенство не выполняется, значит, подпись фальшивая.
. Равенство не выполняется, значит, подпись фальшивая.
Как появилось понятие хэш?
Сделаем небольшую паузу, чтобы интеллект окончательно не поплыл от потока сложных для простых пользователей терминов и информации. Расскажем об истории появления термина «хэш». А для простоты понимания выложим «инфу» в табличной форме.
| Дата (год) | Хронология событий |
| 1953 | Известный математик и программист Дональд Кнут авторитетно считает, что именно в этот промежуток времени сотрудник IBM Ханс Питер Лун впервые предложил идею хеширования. |
| 1956 | Арнольд Думи явил миру такой принцип хеширования, какой знают его подавляющее большинство современных программистов. Именно эта «светлая голова» предложила считать хэш-кодом остаток деления на любое простое число. Кроме этого, исследователь видел идеальное хеширование инструментов для позитивной реализации «Проблемы словаря». |
| 1957 | Статья Уэсли Питерсона, опубликованная в «Journal of Research and Development», впервые серьезно затронула поиск информации в больших файлах, определив открытую адресацию и ухудшение производительности при ликвидации. |
| 1963 | Опубликован труд Вернера Бухгольца, где было представлено доскональное исследование хэш-функции. |
| 1967 | В труде «Принципы цифровых вычислительных систем» авторства Херберта Хеллермана впервые упомянута современная модель хеширования. |
| 1968 | Внушительный обзор Роберта Морриса, опубликованный в «Communications of the ACM», считается точкой отсчета появления в научном мире понятия хеширования и термина «хэш». |
Интересно! Еще в 1956 году советский программист Андрей Ершов называл процесс хеширования расстановкой, а коллизии хэш-функций – конфликтом. К сожалению, ни один из этих терминов не прижился.
Квалифицированная электронная подпись
КЭП – это самый совершенный вид усиленной электронной подписи. Она представляет собой ключ, который формируется с использованием надежных криптографических средств и может применяться для удаленной подачи документов, регистрации онлайн кассы в ФНС, работы с большинством государственных порталов и участия в торгах или приобретения имущества после банкротства владельца.
Получить сертификат, в котором указан ключ электронной подписи можно в удостоверяющем центре, аккредитованном в Минкомсвязи. Для этого потребуется собрать полный пакет уставных документов компании, а также подтвердить личность получателя.
КЭП обеспечивает высокую защиту информационных данных от третьих лиц, при этом установить степень конфиденциальности может сам владелец. Защита данных будет действовать даже тогда, когда его срок действия истечет. Ключ состоит из двух частей:
- проверочного сертификата, который хранится на USB носителе;
- лицензированного дистрибутива, представляющего собой установочный пакет специализированного ПО, который может использоваться на протяжении всего срока действия ключа.
Для того чтобы использовать КЭП потребуется приобрести флеш-накпитель и установить компьютерную программу, например КриптоПро. Функциональность ПО обеспечивается за счет установки личного сертификата и соответствующих библиотек для электронной подписи.
Криптографические хэш-функции в помощь it-юристу
При заключении договоров о распоряжении правами на результаты интеллектуальной деятельности большое значение имеет идентификация объектов, права на которые являются предметом договора.
Поскольку зачастую экземпляры результатов интеллектуальной деятельности (далее — РИД) весьма объёмны в цифровой форме, то классический вариант идентификации в виде, например, распечатывания, не всегда удобен: затруднительно и трудозатратно распечатывать 500 фотографических произведений в высоком качестве, ещё сложнее «распечатать» аудиовизуальное или музыкальное произведение. Про объёмные и сложные программы для ЭВМ и говорить не приходится — у комплексных проектов объём исходного кода зачастую измеряется миллионами строк кода. Например, браузер Google Chromium (на базе которого подготовлен всем известный Chrome) уже в 2021 году содержал более 15 миллионов строк кода.
С учётом таких сложностей, творческая мысль более прогрессивных участников гражданских отношений дошла до возможности приложения одноразовых финализированных компакт-дисков в качестве приложения, при этом указывались «реквизиты» компакт-диска. Однако, такой способ тоже не слишком удобен:
Ещё более прогрессивные участники договорных отношений стали пользоваться всеми возможностями, которые им предоставляет информационно-телекоммуникационная сеть общего пользования «Интернет» — договариваться через VoIP, заключать договоры по электронной почте, обмениваться экземплярами РИД через файлообменные сервисы.
Уже никого не удивляет ситуация, когда контрагенты и их представители друг друга вообще никогда не видели вживую.
Возникает вопрос — чем заменить традиционные «механизмы» по идентификации в соответствии с современными реалиями?
Можно указать ссылку и размер файла, содержащего экземпляр РИД, но ссылка может перестать быть активной или же имеющий возможность участник, может подменить файл по ссылке на другой с идентичным размером. Да и в случае, если речь идёт о «продаже сайта» с контентом (а не только лишь праве администрирования доменного имени), одной лишь ссылки на доменное имя будет явно недостаточно.
Как обойти эти ограничения и избежать подобных рисков?
Автор этого материала нашёл для себя ответ несколько лет назад — криптографические хэш-функции[1].

Понятие хэш-функции
Максимально упростим имеющиеся определения для понимания: хэш-функция — это алгоритм, создающий цифровой «отпечаток» какого-либо исходного сообщения. Под исходным сообщением может пониматься как одна фраза, так и файл в десятки гигабайт. Длина «отпечатка» или хэш-суммы зависит от вида хэш-функции. Хэш-функции очень давно используются программистами для самых разных задач, в числе которых и криптография, и идентификация паролей, файлов, проверка целостности файлов и многое другое.
Например, рассмотрим работу хэш-функции на примере достаточно древнего по компьютерным меркам алгоритма MD5[2].
1.1 Создадим текстовый файл file.txt, содержащий текст ст. 1226 ГК РФ в командной оболочке bash.
ivan@pc ~ $ echo ‘На результаты интеллектуальной деятельности и приравненные к ним средства индивидуализации (результаты интеллектуальной деятельности и средства индивидуализации) признаются интеллектуальные права, которые включают исключительное право, являющееся имущественным право м, а в случаях, предусмотренных настоящим Кодексом, также личные неимущественные права и иные права (право следования, право доступа и другие).’ > file.txt
1.2 Теперь получим MD5-хэш получившегося файла с помощью команды md5sum.
ivan@pc ~ $ md5sum file.txt f9f3b31589779e2b5cfb41bb77cc42d5 file.txt
Вот этот набор букв и цифр «f9f3b31589779e2b5cfb41bb77cc42d5» – и есть уникальный цифровой идентификатор файла. При изменении любого символа, мы получим совершенно иной результат.
2.1 Чтобы убедиться в этом, мы проделаем аналогичные действия, но изменим положение запятой после «право следования».
ivan@pc ~ $ echo ‘На результаты интеллектуальной деятельности и приравненные к ним средства индивидуализации (результаты интеллектуальной деятельности и средства индивидуализации) признаются интеллектуальные права, которые включают исключительное право, являющееся имущественным право м, а в случаях, предусмотренных настоящим Кодексом, также личные неимущественные права и иные права (право следования ,право доступа и другие).’ > file.txt
2.2 А теперь посмотрим, что нам выдаст MD5:
ivan@pc ~ $ md5sum file.txt a61365209311862e668c9666a50b7325 file.txt
Как видно, результат совершенно иной — его невозможно спутать с предыдущим ввиду явных отличий. То есть, малейшее изменение исходного значения – и результирующая хэш-сумма получается другой, что и является идеальным для точной идентификации. Но, как видно, длина хэш-суммы ограничена, а количество файлов – огромно, поэтому есть некоторые сложности.
3.1 Понятие коллизии
Коллизия — это случай одинакового «результата» работы хэш-функции при разных вводных данных. Несмотря на то, что получившиеся в 1.2 и 2.2 хэши очень сильно отличаются, в безграничном цифровом океане файлов невероятно много (и пока Вы читали это предложение — их стало ещё больше), поэтому коллизии неизбежны. Чем более старый алгоритм, тем менее он надёжен и криптоустойчив.
Для примера — для поиска MD5 коллизии достаточно мощности старого ПК или современного смартфона (от нескольких секунд до нескольких минут). Более современный SHA-1 в 2021 году для взлома требовал непрерывной работы на брутфорс (brute force) 12 миллионов видеокарт. Найденная в феврале 2021 года «уязвимость» от Google с названием SHAttered[3] (“shattered” с англ. – “разбитый”) позволяет достичь аналогичных результатов с использованием всего лишь 110 видеокарт.
Что это значит для юристов? Это значит, что для точной и бесспорной идентификации необходимо использовать несколько разных хэш-функций.
Снимем SHA-1 с представленных Google файлов:
ivan@pc ~ $ sha1sum shattered-*
38762cf7f55934b34d179ae6a4c80c
38762cf7f55934b34d179ae6a4c80c
Как видим, хэши SHA-1 одинаковы.
Теперь посмотрим на MD5.
ivan@pc ~ $ md5sum shattered-*
ee4aa52b139d925f8d8884402b0a75
5bd9d8cabc46041579a311230539b8
Так, файлы из примера Google хоть и имеют одинаковые SHA-1 хэши, но в то же время совершенно различные хэши MD5. Кроме того, в статье явно отмечается, что (пока) не существует метода добиваться одновременных коллизий для SHA-1 и MD5.
Поэтому логичный вывод: чем больше различных хэш-функций использовано — тем надёжнее идентификация. Сочетание характеристик точного размера файла, содержащего РИД и нескольких хэш-сумм позволяет однозначно и бесспорно идентифицировать конкретный файл.
При этом указанный файл также может быть и «мета-файлом» – архивом, содержащим любое количество других файлов (например, фотографические произведения или исходный код программы).
Указанный способ представляется более удобным и надёжным по сравнению с остальными:
С учётом того, что программ для калькуляции хэш-сумм огромное количество под любые операционные системы, а в дистрибутивах GNU/Linux они присутствуют в штатной поставке большинства дистрибутивов, единственное препятствие победоносному шествию хэш-функций по приложениям к договорам — желание или нежелание участников гражданского оборота и правоприменителей разбираться в возможностях этих алгоритмов.
- ↑https://habrahabr.ru/post/93226/
- ↑https://ru.wikipedia.org/wiki/MD5
- ↑https://security.googleblog.com/2021/02/announcing-first-sha1-collision.html
Линк на оригинал.
Общие сведения
Криптографическая хеш-функция – это математический алгоритм, который отображает данные произвольного размера в битовый массив фиксированного размера.
Результат, производимый хеш-функцией, называется «хеш-суммой» или же просто «хешем», а входные данные часто называют «сообщением».
Для идеальной хеш-функции выполняются следующие условия:
а) хеш-функция является детерминированной, то есть одно и то же сообщение приводит к одному и тому же хеш-значениюb) значение хеш-функции быстро вычисляется для любого сообщенияc) невозможно найти сообщение, которое дает заданное хеш-значениеd) невозможно найти два разных сообщения с одинаковым хеш-значениемe) небольшое изменение в сообщении изменяет хеш настолько сильно, что новое и старое значения кажутся некоррелирующими
Давайте сразу рассмотрим пример воздействия хеш-функции SHA3-256.
Число 256 в названии алгоритма означает, что на выходе мы получим строку фиксированной длины 256 бит независимо от того, какие данные поступят на вход.
На рисунке ниже видно, что на выходе функции мы имеем 64 цифры шестнадцатеричной системы счисления. Переводя это в двоичную систему, получаем желанные 256 бит.
Любой заинтересованный читатель задаст себе вопрос: “А что будет, если на вход подать данные, бинарный код которых во много раз превосходит 256 бит?”
Ответ таков: на выходе получим все те же 256 бит!
Дело в том, что 256 бит – это
Чтобы прикинуть, насколько велико это значение, запишем его следующим образом:
Надеюсь, теперь нет сомнений в том, что это очень внушительное число!
Поэтому ничего не мешает нам сопоставлять длинному входному массиву данных массив фиксированной длины.
Первый учебный алгоритм хеширования
Входом для данного алгоритма является строка, состоящая из букв русского языка.
Выбирается число
 – вектор инициализации. Число
– вектор инициализации. Число  равно длине сообщения в символах.
равно длине сообщения в символах.Для каждого символа сообщения вычисляется значение
 , где
, где 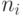 – номер
– номер  -й буквы сообщения в алфавите. Для удобства вычислений ниже приведен нумерованный алфавит.
-й буквы сообщения в алфавите. Для удобства вычислений ниже приведен нумерованный алфавит.- Значение
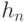 , вычисленное для последнего символа, является хеш-значением сообщения:
, вычисленное для последнего символа, является хеш-значением сообщения: 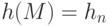 .
.
Следует отметить, что вычисленное по этому алгоритму хеш-значение зависит от всех символов сообщения 
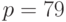
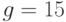


 Пример 9.2Выполнить вычисление и проверку подписи сообщения
Пример 9.2Выполнить вычисление и проверку подписи сообщения  по алгоритму Эль-Гамаля. Использовать параметры подписи:
по алгоритму Эль-Гамаля. Использовать параметры подписи:
- Сформируем хэш-сумму сообщения. Начальное значение
 равно количеству символов сообщения:
равно количеству символов сообщения:  . Далее,
. Далее, - Вычисляем число
 по формуле
по формуле 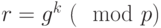 . Для рассматриваемого примера получили:
. Для рассматриваемого примера получили: - Вычисляем число
 по формуле
по формуле  , для рассматриваемого примера
, для рассматриваемого примера - Вычисляем значение
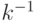 по модулю
по модулю  с помощью расширенного алгоритма Евклида. Для рассматриваемого примера значение
с помощью расширенного алгоритма Евклида. Для рассматриваемого примера значение  .
.Примечание: если полученное значение
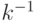 – отрицательное, следует взять его по модулю
– отрицательное, следует взять его по модулю  .
. - Вычисляем число
 по формуле
по формуле 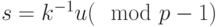 . В примере
. В примере - Цифровая подпись сообщения для рассматриваемого примера:
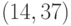 .
.
Для проверки правильности вычисления полученной цифровой подписи следует произвести ее проверку с помощью открытого ключа абонента и убедиться, что подпись подлинная.
- Сформируем открытый ключ
 абонента по формуле
абонента по формуле 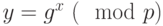 :
:Для рассматриваемого примера
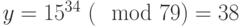 .
. Аналогичным образом вычисляем значения
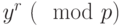 и
и  , а затем их произведение по модулю
, а затем их произведение по модулю  .
.В примере получаем:
- Вычисляем значение
 , значение
, значение  было получено ранее.
было получено ранее.В примере
 .
. - Проверяем выполнение равенства
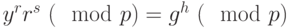 , если равенство выполняется – подпись подлинная, то есть она была вычислена правильно.
, если равенство выполняется – подпись подлинная, то есть она была вычислена правильно.В примере получили
 , равенство выполняется, значит, подпись сгенерирована правильно.
, равенство выполняется, значит, подпись сгенерирована правильно.
Практическое применение
Процедура хеширования относительно своего функционала может быть нескольких типов:
- Протокол для аудита целостности информации. В процессе передачи документов осуществляется вычисления хэш-кода. Результат передается вместе с документами. Прием информации сопровождается повторным вычислением хэш-кода с последующим сравнением, полученным значением. Несовпадение – ошибка. Этот алгоритм обладает высокими скоростными показателями при вычислении, но отличается нестабильностью и малым значением хэш-функции. Пример – протокол CRC-32, который имеет только 232 значения хэш, различающихся между собой.
- Криптографический алгоритм. Внедряется в качестве защиты от несанкционированного доступа (взлома). Проверяет систему на предмет искажения информации в момент передачи файлов по сети. При таких обстоятельствах «правильный» хэш имеет свободный доступ, а ключ, полученного документа, вычисляется при помощи разнообразных софтов (программ). Пример – SHA-1, SHA-2, MD5, отличающихся стабильностью и сложнейшим уравнением поиска коллизий.
- Протокол для создания эффективной информационной конструкции. Определяющая задача – структурирование информации в хэш-таблицы. Такая табличная структура делает возможным добавлять/удалять, находить нужные данные с невероятной скоростью.
Разберемся детальней в сфере применения протоколов хеширования.
Принцип работы эцп
Объяснить механизм работы этого электронного продукта можно простыми словами, поскольку он достаточно прост и понятен. Когда производится непосредственное подписание документа, создается особый блок данных, который и называют ЭЦП. Процесс его образования происходит поэтапно.
- отпечаток не может использоваться для восстановления тела документа;
- при создании разных сообщений отпечаток уникален, а длина его фиксирована.
Во время второго этапа происходит шифрование отпечатка при помощи программы и ключа. Для его расшифровки в последующем подойдет только открытый личный ключ электронной подписи.
При получении электронных документов принцип работы ЭЦП, следующий:
- используя специальную программу, адресат расшифровывает документы, подписанные при помощи ЭЦП с целью восстановления отпечатка исходных данных;
- при взаимодействии функции хэширования с ПО производится вычисление информации и создание исходного отпечатка документа;
- для сравнения полученного и исходного отпечатка производится высокоточная проверка информации.
Если во время процесса не возникло ошибок и отпечатки оказались абсолютно идентичными, то ЭЦП подтверждает верность, а также целостность полученного документа. Если же при пересылке были произведены какие-либо изменения или нарушена целостность исходного документа, это отразится при получении результата.
К наиболее важным моментам при работе электронной подписи можно отнести отметку времени подписания документа. С ее помощью можно точно узнать, в какой момент был создан файл. Если автору необходимо внести какие-то изменения в документ после того, как поставлена отметка, после исправления ему потребуется поставить подпись заново, а значит обновится и информация о времени создания. Во время подписания происходит синхронизация данных со Всемирным координированным временем.
Простая электронная подпись
Простую электронную подпись, которая требуется для авторизации на интернет-ресурсах, заверения документов и получения доступа к защищенным базам данным, можно получить несколькими способами:
- Посредством офисного пакета приложений Microsoft Office. Для этого после создания документа нужно будет зайти в меню «Файл» и остановится на пункте «Защита документа», после чего нажать на «Добавить цифровую подпись». При первичном получении программа запросит произвести установку специализированного ПО от партнеров. Для установления подписи в операционную систему можно воспользоваться небольшим приложением «Карма».
- С помощью приложения КриптоПро CSP. Этот способ немного сложнее первого, однако он позволяет пользователям создавать усиленные ключи.
- USB-токен – один из способов получения заверенной ПЭП, предусматривающий посещение удостоверяющего центра, специалисты которого запишут сертификат на USB. Это оптимальный вариант для тех, кто работает в текстовых редакторах и желает подтвердить авторство или защитить документы от плагиата.
Основным недостатком такой подписи является то, что она не имеет юридической силы. Она не подойдет для подачи документации в государственные организации и для участия в электронных торгах. Чтобы ее использовать для подписания документации, например с контрагентами, требуется составить и подписать соглашение, содержащее пункты о необходимости соблюдения конфиденциальности данных и правила определения подлинности. Такой документ должны подписать все стороны, принимающие участие в электронном взаимодействии.
Стандарты хеширования: популярные варианты
Итак, от экскурса в историю перейдем вновь к серьезной теме. Опять-таки, ради простоты восприятия предлагаем краткое описание популярных стандартов хеширования в табличном виде. Так проще оценить информацию и провести сравнение.
| Название | Краткий обзор |
| CRC-32 | Полином CRC (Cyclic Redundancy Check, что значит «циклическая проверка излишков»). Является мощным легко осуществимым методом хеширования для достижения надежности информации. Применяется для защиты данных и обнаружении ошибок в потоке информации. Популярность принесли следующие качества: высочайшая степень обнаружения ошибок, минимальные расходы, простота эксплуатирования. Генерирует 32-битный хэш. Используется комитетом по стандартам локальных систем. |
| MD5 | Протокол базируется на 128-битном (16-байтном) фундаменте. Применяется для хранения паролей, создания уникальных криптографических ключей и ЭЦП. Используется для аудита подлинности и целостности документов в ПК. Недостаток – сравнительно легкое нахождение коллизий. |
| SHA-1 | Реализует хеширование и шифрование по принципу сжатия. Входы такого алгоритма сжатия состоят из набора данных длиной 512 Бит и выходом предыдущего блока. Количество раундов – 80. Размер значения хэш – 32 Бит. Найденные коллизии – 252 операции. Рекомендовано для основного использования в госструктурах США. |
| SHA-2 | Семейство протоколов – однонаправленных криптографических алгоритмов, куда входит легендарный SHA-256, используемый в Bitcoin. Размер блока – 512/1024 Бит. Количество раундов 64/80. Найденных коллизий не существует. Размер значения однонаправленных хэш-функций – 32 Бит. |
| ГОСТ Р 34.11-2021 «Стрибог» | Детище отечественных программистов, состоящее из пары хэш-функций, с длинами итогового значения 256 и 512 Бит, отличающиеся начальным состоянием и результатом вычисления. Криптографическая стойкость – 2128. Преобразование массива данных основано на S-блоках, что существенно осложняет поиск коллизий. |
На этом, пожалуй, закончим экскурсию в мир сложных, но весьма полезных и востребованных протоколов хеширования.
Функция перестановок
Базовая функция перестановки состоит из
Шаг
Шаг
Шаг
Шаг
Шаг
Тета, Ро, Пи, Хи, Йота
Далее будем использовать следующие обозначения:
Так как состояние
Я хочу вкратце описать каждый шаг функции перестановок, не вдаваясь в математические свойства каждого.
Шаг Эффект отображения
Схематическое представление функции:
Псевдокод шага:
Шаг
Проще всего его описать псевдокодом и схематическим рисунком:
ШагШаг
Псевдокод и схематическое представление:
Шаг Отображение
Все шаги можно объединить вместе и тогда мы получим следующее:
Где константы
Электронная подпись для чайников: с чем ее есть и как не подавиться. часть 2
Продолжая раскрывать тайное знание о цифровой подписи простым языком, разберем, что же нам надо для удобной и эффективной работы с ними, а также главное различие между лагерями S/MIME X.509 и PGP.
Перед тем, как рассматривать особенности этих двух больших лагерей, стоит рассмотреть, какая информация нужна получателю для проверки подписи (а наш зашифрованный хэш уже вполне можно называть подписью), и в каком виде ее можно ему передать.
Каждую из частей информации можно передать вместе с открытым ключом, или вместе с нашей подписью, а можно и с тем и с тем, для большего удобства. Конечно, можно не разделять информацию на передаваемую с открытым ключом и передаваемую с подписью. Но тогда каждый раз отправляя подписанную информацию мы отправляем одно и то же. Как если бы к каждому отправляемому нами бумажному письму (даже короткому, в две строки), мы бы прикладывали дополнение вида «Здравствуйте! Это я, В. Пупкин, которого вы встречали на Красной площади Москвы, где мы и познакомились, потом пошли в ресторан, потом <…>». Согласитесь, слегка неудобно.
Но вернемся к нашей информации, необходимой для проверки подписи.
Начнем с простого: информация, которая позволит нам узнать, кто же сделал эту подпись. Как мы уже договорились, ассиметричное шифрование позволяет однозначно связать наш открытый ключ и полученную подпись. Беда в том, что сам по себе открытый ключ – набор байт. При этом он, конечно, связан с закрытым, которым мы (то есть отправитель) владеем, но связь эта для получателя неочевидна. У него есть набор байт от В. Пупкина, от И. Петрова, от С. Сидорова… И от десятка других людей. И как ему их идентифицировать? Держать отдельный реестр для того, кому какой набор байт принадлежит? Это что же, получается уже второй реестр (помимо того, где должно быть записано, с помощью какой хэш-функции какой хэш сделан)! И опять, неудобно!
Значит, надо связать каждый открытый ключ с информацией о том, кому этот ключ принадлежит, и присылать это все одним пакетом. Тогда проблема реестра решается сама собой – пакет (а если более правильно, контейнер) с открытым ключом можно будет просто посмотреть и сразу понять его принадлежность.
Но эту информацию все так же надо связать с подписью, пришедшей получателю. Как это сделать? Надо соорудить еще один контейнер, на сей раз для передачи подписи, и в нем продублировать информацию о том, кто эту подпись создавал.
Продолжая нашу аналогию с красивым замком, мы пишем на ключе «Этот ключ открывает замок В. Пупкина». А на замке тоже пишем «Замок В. Пупкина». Имея такую информацию, получатель нашей коробочки не будет каждый из имеющихся у него ключей вставлять наугад в наш замок, а возьмет наш ключ и сразу его откроет.
Теперь, по переданной информации при проверке можно найти контейнер открытого ключа, взять оттуда ключ, расшифровать хэш и…
А собственно, что «и»? Мы ведь пока так и не решили проблему, как донести до получателя информацию о том, какая хэш-функция применялась для хэша, а ведь для проверки подписи эта информация необходима! Решить ее можно достаточно просто: положить эту информацию в контейнер вместе с нашим открытым ключом. Ведь именно связка «хэширование – шифрование результата хеширования» считается процедурой создания цифровой подписи, а ее результат – подписью. А значит, достаточно логичным представляется объединение в связку алгоритма шифрования хэша и хэш-функции, с помощью которой он сформирован. И доставлять эту информацию тоже надо в связке.

Теперь, ненадолго вернемся к информации о подписывающем. Какого рода эта информация должна быть? ФИО? Нет, В. Пупкиных много. ФИО год рождения? Так и родившихся в один день В. Пупкиных тоже предостаточно! Более того, это может быть Василий, Виктор, или даже Василиса или Виктория Пупкины. Значит, информации должно быть больше. Ее должно быть столько, чтобы совпадение всех параметров, по которым мы идентифицируем человека, было максимально невероятным.
Безусловно, такой пакет информации создать возможно. Вот только, работать с ним уже трудновато. Ведь надо наши контейнеры открытых ключей надо сортировать, хранить, использовать, в конце концов. А если для каждого использования придется указывать по полсотни параметров, то уже на втором контейнере станет понятно, что что-то надо менять. Решение этой проблемы, конечно же, было найдено.
Чтобы понять, в чем же оно заключалось, обратимся к бумажному документу, который есть у всех нас: к паспорту. В нем можно найти и ФИО, и дату рождения, и пол, и много другой информации. Но, главное, в нем можно найти серию и номер. И именно серия и номер являются той уникальной информацией, которую удобно учитывать и сортировать. Кроме того, они существенно короче всей оставшейся информации вместе взятой, и при этом все так же позволяют опознать человека.
Применяя этот же подход к контейнерам открытых ключей, мы получим, что у каждого контейнера должен быть некий номер, последовательность символов, уникальная для него. Эту последовательность символов принято называть идентификатором, а сами контейнеры – сертификатами, либо просто ключами.
Вот здесь и начинаются принципиальные различия в идеологиях OpenPGP и S/MIME X.509. Для краткого понимания их, вернемся к нашей аналогии с паспортом.
Паспорт вы можете использовать при покупках билетов, при оформлении документов, для выдачи пропуска на какую-либо территорию и даже на территории других стран! То есть, вы используете его для идентификации вашей личности в самых различных, зачастую абсолютно не связанных друг с другом, местах, с самыми различными людьми. И везде ваш паспорт принимают. Гарантом того, что вы – это вы выступает третья сторона в ваших взаимоотношениях с другими: государство. Именно оно выдало вам ваш паспорт, специально оформленный, подписанный и заверенный, и именно поэтому ваш паспорт является таким универсальным документом.
С другой стороны, в кругу друзей, или внутри компании вам достаточно представиться так: «В. Пупкин из твоей группы в институте» или же «В. Пупкин из отдела продаж». И людям, с которыми вы контактируете в этом кругу уже не нужна третья сторона, они и так помнят Пупкина из группы с которым проучились пять лет, или Пупкина из отдела продаж, с которым недавно ходили обедать, и предоставленной вами информации им вполне достаточно.
Так же можно разделить и эти два лагеря.
Сертификат X.509 – это аналог нашего паспорта. Здесь сертификаты вам выдаются суровой третьей стороной, гарантом вашей личности: Удостоверяющим Центром (УЦ). Получающий ваши подписи человек всегда может обратиться в УЦ и спросить интересующую его информацию по вот этому конкретному сертификату.
PGP же (и стандарт OpenPGP, появившийся в дальнейшем) создавался на основе так называемых сетей доверия. Такая идея подразумевает, что обмениваются подписями люди, которым третья сторона для их взаимоотношений не нужна, а нужна только защита от нехороших лиц.
Конечно, с течением времени такое разделение стало уже достаточно условным, так как на данный момент и в S/MIME X.509 и в PGP можно использовать методы лагеря соперников. Но все же, стандарты достаточно продолжительное время развивались параллельно и развились до той степени, что взаимная совместимость между ними стала невозможной.
Более популярным стандартном, в силу своей ориентированности на участие более компетентной третьей стороны, стал стандарт S/MIME X.509, однако и у PGP есть некоторое количество козырей за пазухой, с помощью которых он не только не погибает, но и продолжает успешно развиваться.
Более подробное рассмотрение каждого из форматов, а также рекомендации, когда, где и какой из них использовать вы сможете прочитать уже в следующих статьях.
Часть 3





