НОУ ИНТУИТ | Лекция | Криптографические алгоритмы с открытым ключом и их использование

Генерация ключей

Генерация ключей в схеме цифровой подписи RSА точно такая же, как и генерация ключей в криптографической системе RSА (см.

“B. Стандарты и организации по стандартизации”
). Алиса выбирает два простых числа p и q и вычисляет n = p x q. Алиса вычисляет e, для общедоступного ключа и вычисляет d для частного ключа, такое, что d и публично объявляет n и e.

В схеме цифровой подписи RSA. dявляется частным;. eи. n- общедоступными.

Подписание и проверка

Рис 3.7 показывает схему цифровой подписи RSA.

Подписание. Алиса на основе сообщения создает подпись, используя частный (секретный) ключ, S = Md mod n, и передает сообщение и подпись Бобу.

Проверка. Боб получает М и S. Он применяет общедоступный ключ Алисы к подписи, чтобы создать копию сообщения М’ = Se mod n. Боб сравнивает значение М’ со значением М.

Последняя конгруэнтность справедлива, потому что
“A. ASCII”
).

Пример 3.1

Для безопасности подписи значения p и q должны быть очень большими. Как тривиальный пример, предположим, что Алиса выбирает p = 823 и q = 953 и вычисляет n = 784319. Значение 782544. Теперь она выбирает e = 313 и вычисляет d = 160009. В этой точке генерация ключей закончена. Теперь вообразим, что Алиса хочет передать сообщение со значением M = 19070 Бобу. Она использует свой частный ключ 160009 для того, чтобы подписать сообщение:

Алиса передает сообщение и подпись Бобу. Боб получает сообщение и подпись. Он вычисляет

Боб принимает сообщение, потому что он проверил подпись Алисы.

Атаки подписи RSA

Есть некоторые атаки, к которым Ева может обратиться для подделки схемы цифровой подписи RSА Алисы.

Атака только на ключ. Ева имеет доступ только к открытому ключу Алисы, перехватывает пару ( М, S ) и пробует создать другое сообщение М.’, такое, что М’ = Se mod n.

Эта проблема по сложности решения равна проблеме дискретного логарифма, которую мы рассмотрели в

“A. ASCII”
. Это – экзистенциальная подделка и обычно бесполезна для Евы.

Атака при известном сообщении. Здесь Ева использует мультипликативное свойство RSА. Предположим, что Ева перехватила две пары подписи сообщения – (M1, S1) и (M2, S2), которые используют один и тот же секретный ключ.

S = S1 x S2 mod n =
(M1d x M2d) mod n =
(M1 x M2)d mod n =
Md mod n

Ева может создать М. = M1 x M2 mod n и может создать S. = S1 x S2 mod n ; глупый Боб поверит, что S – подпись Алисы на сообщении М.

Эта атака, которая называется иногда мультипликативной атакой,
проводится очень просто. Однако это – экзистенциальная подделка так, как сообщение, М является произведением двух предыдущих сообщений, созданных Алисой, а не Евой; сообщение М. обычно бесполезно.

Атака по выбранному сообщению. Эта атака также использует мультипликативное свойство RSA. Ева может так или иначе попросить, чтобы Алиса подписала два законных сообщения М1 и М2.

С помощью их она позже создает новое сообщение М. = M1 x M2. Ева может позже утверждать, что Алиса подписала M. Такую атаку называют так же, как и
предыдущую – мультипликативная атака.

Это очень серьезная атака схемы цифровой подписи RSA, потому что это – селективная подделка. (Ева может перемножать М1 и М2, чтобы получить полезный M ).

Подпись RSA на дайджесте сообщения

Как мы обсуждали прежде, подписание дайджеста сообщения и использование сильного алгоритма хэширования имеет несколько преимуществ. В случае RSA процессы подписания и проверки можно сделать намного быстрее, потому что схема цифровой подписи RSА – не что иное, как шифрование с секретным ключом и дешифрование с открытым ключом.

Алиса, подписывающее лицо, при первом использовании согласует
хэш-функцию, чтобы создать дайджест сообщенияD = h(M). Затем она подписывает дайджест, S = Dd mod n.

Сообщение и подпись передают Бобу. Боб, проверяющий, получает сообщение и подпись. Он сначала использует открытый ключ Алисы, чтобы извлечь (файл) дайджест, D’ = Se mod n. Затем он применяет хэш-алгоритм для того, чтобы получить сообщение D = h(M).

Боб теперь сравнивает эти два дайджеста, D и D’. Если они являются сравнимыми по модулю n, он принимает сообщение.

Атаки на подписанные дайджесты RSA

Насколько восприимчива схема цифровой подписи RSA к нападению, когда дайджест уже подписан?

Атака только на ключ. Мы можем иметь три случая этой атаки.

1. Ева перехватывает пару (S, M) и пробует найти другое сообщение М’, которое создает тот же самый дайджест, h (M) = h (М’). Как мы узнали в
   
   “Целостность сообщения и установление подлинности сообщения”
   , если алгоритм хэшированияобладает устойчивостью ко второму прообразу,
   эта атака очень трудна.
2. Ева находит два сообщения, М. и М’, такие, что h(M) = h(M’). Она соблазняет Алису подписать h(M), чтобы найти S ; теперь Ева имеет пару (М’, S), которое прошло подтверждающий тест, но это – подделка. Мы изучали в
   
   “Целостность сообщения и установление подлинности сообщения”
   , что если алгоритм хэшированияустойчив к коллизиям, эта атака очень трудна.
3. Ева случайным подбором может найти дайджест сообщения D, который может соответствовать случайной подписи S. Она тогда находит сообщение М, такое, что D = h (M). Как мы узнали в
   
   “Целостность сообщения и установление подлинности сообщения”
   , если хэш-функция устойчива к прообразу, эта атака очень трудно осуществима.

Атака при известном сообщении. Предположим, что Ева имеет две пары подписи сообщения – (М1,S1) и (М2, S2), которые были созданы с использованием одного и того же секретного ключа.

Ева вычисляет S = S1 x S2. Если она сможет найти сообщение М, такое, что h(M) = h(M1) x h(M2), она сможет подделать новое сообщение.

Атаки по выбранному сообщению. Ева может попросить, чтобы Алиса подписала два законных сообщения – М1,и М2 для нее. Она может создать новую подпись S = S1 x S2.

Так как Ева может вычислить h(M) = h(M1) x h(M2), если она может найти сообщение M данному h (M), это новое сообщение – подделка. Однако нахождение М по данному h (M) -очень трудный процесс, если алгоритм хэшированияустойчив к прообразу.

Когда дайджест подписан непосредственно вместо сообщения, восприимчивость. схемы цифровой подписи RSAзависят от свойств алгоритма хэширования.

Криптографические системы на эллиптических кривых

В 1985 году американские ученые Н. Коблиц (Neal Koblitz) и В. Миллер (Victor Miller) предложили использовать для криптосистем с открытым ключом теорию эллиптических кривых. Дальнейшие исследования подтвердили наличие подходящих свойств у этих математических функций и привели к созданию реальных криптографических систем, использующих математический аппарат эллиптических кривых.

С 1998 года использование эллиптических кривых для решения криптографических задач, таких, как цифровая подпись, было закреплено в стандартах США ANSI X9.62 и FIPS 186-2, а в 2001 году аналогичный стандарт, ГОСТ Р34.10-2001, был принят и в России.

Основное достоинство криптосистем на эллиптических кривых состоит в том, что по сравнению с другими асимметричными криптосистемами, рассмотренными нами ранее, они обеспечивают существенно более высокую криптостойкость при равных затратах на обработку и вычисления.

Это объясняется тем, что вычисление обратных функций на эллиптических кривых значительно сложнее, чем, например, вычислениедискретных логарифмов (алгоритмы Диффи-Хеллмана и Эль-Гамаля) или решение задачи факторизации (алгоритмRSA).

В результате тот уровень стойкости, который достигается, скажем, в RSA при использовании 1024-битовых модулей, в системах на эллиптических кривых реализуется при размере модуля 160 бит, что обеспечивает более простую как программную, так и аппаратную реализацию.

Криптография эллиптических кривых использует достаточно сложный аппарат высшей алгебры, поэтому мы, в рамках данного учебного пособия, не сможем подробно рассмотреть используемые на практике алгоритмы и выполнить соответствующие примеры вычислений. Сформулируем основные принципы построения криптографических систем с использованием эллиптических кривых.

В криптографии используются эллиптические кривые на плоскости, определяемые уравнениями вида

где р – некоторое большое простое число, а a и b – константы. График эллиптической кривой при разных значениях параметров а и b имеет вид, как на
рис.
11.1.

Принцип использования эллиптических кривых следующий. Для группы пользователей выбирается общая эллиптическая криваяЕ и некоторая точка G на ней. Закрытым ключом пользователя выступает некоторое целое числос, а открытым – точка D на кривой Е, полученная в результате специального преобразования композиции с использованием числа с.

Параметры кривой и список открытых ключей абонентов, как и обычно, передаются всем пользователям сети. Открытые и закрытые ключи пользователей используются для выполнения операций шифрования и расшифрования в зависимости от назначения алгоритма.

С помощью эллиптических кривых могут быть реализованы многие известные протоколы с открытым ключом. Любая криптосистема, основанная на дискретном логарифмировании, легко может быть перенесена на эллиптические кривые.

Например, можно заменить математические операции вида у = gхmod р на операции математического аппарата эллиптических кривых (операции вычисления композиции точек) в алгоритмах формирования ключа Диффи-Хеллмана или вычисления цифровой подписи Эль-Гамаля. В результате получатся те же алгоритмы, но с другими математическими операциями.

Несмотря на сложность математического аппарата эллиптических кривых, существуют эффективные вычислительные методы, позволяющие достаточно быстро реализовывать необходимые расчеты. За счет использования модуля меньшей длины операции генерации ключей и шифрования выполняются быстрее, чем, скажем, в алгоритме RSA или классическом алгоритме Диффи-Хеллмана.

Подпись сообщений

Для подписи сообщения M{displaystyle M} выполняются следующие операции:

1. Вычисляется дайджест сообщенияM{displaystyle M}: m=h(M).{displaystyle m=h(M).}(Хеш функция может быть любая).
2. Выбирается случайное число 1<k<p−1{displaystyle 1<k<p-1} взаимно простое с p−1{displaystyle p-1} и вычисляется r=gkmodp.{displaystyle r=g^{k},{bmod {,}}p.}
3. Вычисляется число s=(m−xr)k−1(modp−1){displaystyle s,=,(m-xr)k^{-1}{pmod {p-1}}}, где k−1{displaystyle k^{-1}} это мультипликативное обратное k{displaystyle k} по модулю p−1{displaystyle p-1}, которое можно найти, например, с помощью расширенного алгоритма Евклида.
4. Подписью сообщения M{displaystyle M} является пара (r,s){displaystyle left(r,sright)}.

Пример

• Шифрование
  1. Допустим, что нужно зашифровать сообщение M=5{displaystyle M=5}.
  2. Произведем генерацию ключей:
     1. Пусть p=11,g=2{displaystyle p=11,g=2}. Выберем x=8{displaystyle x=8} – случайное целое число x{displaystyle x} такое,что 1<x<p{displaystyle 1<x<p}.
     2. Вычислим y=gxmodp=28mod11=3{displaystyle y=g^{x}{bmod {p}}=2^{8}{bmod {11}}=3}.
     3. Итак, открытым ключом является тройка (p,g,y)=(11,2,3){displaystyle (p,g,y)=(11,2,3)},а закрытым ключом – число x=8{displaystyle x=8}.
  3. Выбираем случайное целое число k{displaystyle k} такое, что 1 < k < (p − 1). Пусть k=9{displaystyle k=9}.
  4. Вычисляем число a=gkmodp=29mod11=512mod11=6{displaystyle a=g^{k}{bmod {p}}=2^{9}{bmod {11}}=512{bmod {11}}=6}.
  5. Вычисляем число b=ykMmodp=395mod11=19683⋅5mod11=9{displaystyle b=y^{k}M{bmod {p}}=3^{9}5{bmod {11}}=19683cdot 5{bmod {11}}=9}.
  6. Полученная пара (a,b)=(6,9){displaystyle (a,b)=(6,9)} является шифротекстом.
• Расшифрование
  1. Необходимо получить сообщение M=5{displaystyle M=5} по известному шифротексту (a,b)=(6,9){displaystyle (a,b)=(6,9)} и закрытому ключу x=8{displaystyle x=8}.
  2. Вычисляем M по формуле: M=b(ax)−1modp=9(68)−1mod11=5{displaystyle M=b(a^{x})^{-1}{bmod {p}}=9(6^{8})^{-1}mod {11}=5}
  3. Получили исходное сообщение M=5{displaystyle M=5}.

Так как в схему Эль-Гамаля вводится случайная величина k{displaystyle k},то шифр Эль-Гамаля можно назвать шифром многозначной замены. Из-за случайности выбора числа k{displaystyle k} такую схему еще называют схемой вероятностного шифрования. Вероятностный характер шифрования является преимуществом для схемы Эль-Гамаля, так как у схем вероятностного шифрования наблюдается большая стойкость по сравнению со схемами с определенным процессом шифрования. Недостатком схемы шифрования Эль-Гамаля является удвоение длины зашифрованного текста по сравнению с начальным текстом. Для схемы вероятностного шифрования само сообщение M{displaystyle M} и ключ не определяют шифротекст однозначно. В схеме Эль-Гамаля необходимо использовать различные значения случайной величины k{displaystyle k} для шифровки различных сообщений M{displaystyle M} и M′{displaystyle M’}. Если использовать одинаковые k{displaystyle k}, то для соответствующих шифротекстов (a,b){displaystyle (a,b)} и (a′,b′){displaystyle (a’,b’)} выполняется соотношение b(b′)−1=M(M′)−1{displaystyle b(b’)^{-1}=M(M’)^{-1}}. Из этого выражения можно легко вычислить M′{displaystyle M’}, если известно M{displaystyle M}.

Проверка подписи

Зная открытый ключ (p,g,y){displaystyle left(p,g,yright)}, подпись (r,s){displaystyle left(r,sright)} сообщения M{displaystyle M} проверяется следующим образом:

1. Проверяется выполнимость условий: 0<r<p{displaystyle 0<r<p} и 0<s<p−1{displaystyle 0<s<p-1}.
2. Если хотя бы одно из них не выполняется,то подпись считается неверной.
3. Вычисляется дайджест m=h(M).{displaystyle m=h(M).}
4. Подпись считается верной, если выполняется сравнение:

   yrrs≡gm(modp).{displaystyle y^{r}r^{s}equiv g^{m}{pmod {p}}.}

Расшифрование

Зная закрытый ключ x{displaystyle x}, исходное сообщение можно вычислить из шифротекста (a,b){displaystyle (a,b)} по формуле:

M=b(ax)−1modp.{displaystyle M=b(a^{x})^{-1}{bmod {p}}.}

При этом нетрудно проверить, что

(ax)−1=g−kxmodp{displaystyle (a^{x})^{-1}=g^{-kx}{bmod {p}}}

и поэтому

b(ax)−1=(ykM)g−xk≡(gxkM)g−xk≡M(modp){displaystyle b(a^{x})^{-1}=(y^{k}M)g^{-xk}equiv (g^{xk}M)g^{-xk}equiv M{pmod {p}}}.

Для практических вычислений больше подходит следующая формула:

M=b(ax)−1=ba(p−1−x)(modp){displaystyle M=b(a^{x})^{-1}=ba^{(p-1-x)}{pmod {p}}}

Стандарт цифровой подписи (dss)

Стандарт цифровой подписи (DSS – Digital Signature Standard) был принят национальным Институтом Стандартов и Технологии (NIST) в 1994 г. NIST издал DSS как FIPS-186 (FEDERAL INFORMATION PROCESSING STANDARD 186).

DSS применяет алгоритм цифровой подписи (DSA), основанный на схеме Эль-Гамаля, с использованием некоторых идей из схемы Шнорра. DSS критиковался со времени его издания.

В процессе подписания две функции создают две подписи; в процессе проверки выход одной функции сравнивается с первой подписью для проверки. Это подобно схеме Шнорра, но входы различны. Другое отличие: эта схема использует дайджест сообщения (не само сообщение) как часть входов к функциям 1 и 3.

Интересно то, что схема применяет два общедоступных модуля: p и q. Функции 1 и 3 используют оба модуля p и q, функция 2 – только q. Детали входов и функций коротко рассматриваются ниже.

Генерация ключей

Перед подписанием сообщения к любому объекту Алиса должна генерировать ключи и объявить общедоступные ключи.

1. Алиса выбирает простое число длиной p. между 512 и 1024 битами. Число битов в p должно быть кратно числу 64.
2. Алиса выбирает простое число на 160 битов q с таким условием, чтобы оно делилось на (p – 1).
3. Алиса использует две группы умножения, <Z_p*, x > и <Z_q* ,x > ; вторая – подгруппа первой.
4. Алиса создает e₁, такое, чтобы оно было q -тым корнем 1 по модулю p (e₁^p = 1 mod p). Она поступает так: выбирает элемент в Z_p, e₀, и вычисляет e₁ = e₀^(p-1)/q mod p.
5. Алиса выбирает d как секретный ключ и вычисляет e₂ = e₁^d
6. Общедоступный ключ Алисы – (e₁, e₂, p, q), ее секретный ключ – (d).

Подписание и проверка

Рисунок 3.14 показывает схему DSS.

Подписание. Ниже показаны шаги подписания сообщения.

1. Алиса выбирает случайное число (1 <= r <= q). Обратите внимание, что хотя открытые и секретные ключи могут быть выбраны один раз и использоваться для того, чтобы подписать много сообщений, Алиса должна выбирать каждый раз новый r, когда она должна подписать новое сообщение.
2. Алиса вычисляет первую подпись S₁ = (e₁ mod p) mod q. Обратите внимание: значение первой подписи не зависит от М (сообщения).
3. Алиса создает дайджест сообщенияh (M).
4. Алиса вычисляет вторую подпись S₂ = (h(M) dS₁)r^-1mod q. Обратите внимание, что вычисление S₂ делается по модулю q.
5. Алиса посылает M, S₁ и S₂ Бобу.

Проверка (верификация). Для проверки сообщения обычно применяются следующие шаги, когда получены М, S1 и S2.

1. Боб проверяет S₁ 0 < S₁ < q.
2. Боб проверяет S₂ 0 < S₂ < q.
3. Боб вычисляет дайджест М, применяя алгоритм хэширования, используемый Алисой.
4. Боб вычисляет V = [(e₁^h(M)/S2 e₂^S1/S2) mod p] mod q.
5. Если S конгруэнтен V, сообщение принимается; иначе – отклоняется.

Пример 3.5

Алиса выбирает q = 101 и p = 8081. Алиса выбирает e0 = 3 и вычисляет e1 = e0(p-1)/q mod p = 6968.

Алиса выбирает d = 61 в качестве секретного ключа и вычисляет e2 = e1d mod p = 2038. Теперь Алиса может передать сообщение Бобу. Предположим, что h (M) = 5000, и Алиса выбирает r = 61:

Поскольку Sj и V являются подходящими, Боб принимает сообщение.

Сравнение DSS и RSА

Вычисление DSS-подписи быстрее, чем вычисление подписей RSА, при использовании того же самого p.

Сравнение DSS и схемы Эль-Гамаля

DSS-подпись – меньше, чем подписи в схеме Эль-Гамаля, потому что q меньше, чем p.

Схема цифровой подписи шнорра

Проблема схемы цифровой подписи Эль-Гамаля – в том, что p должно быть очень большим, чтобы сделать трудной проблему дискретного логарифмаZp*.

Рекомендуется длина p по крайней мере 1024 битов. Можно сделать подпись размером 2048 бит. Чтобы уменьшить размер подписи, Шнорр предложил новую схему, основанную на схеме Эль-Гамаля , но с уменьшенным размером подписи.
рис. 3.11 дает общую идею схемы цифровой подписи Шнорра.

В процессе подписания две функции создают две подписи; в процессе проверки выход одной функции сравнивается с первой подписью для проверки.
рис. 3.11 показывает входы к каждой функции. Важно то, что схема использует два модуля: p и q.

Генерация ключей

Перед подписанием сообщения Алиса должна генерировать ключи и объявить всем общедоступные ключи.

1. Алиса выбирает простое число p, которое обычно равно по длине 1024 битам.
2. Алиса выбирает другое простое число q, которое имеет тот же самый размер, что и дайджест, созданный функцией криптографического хэширования (в настоящее время 160 битов, но это может измениться в будущем). Простое число q должно делиться на (p – 1). Другими словами, (p – 1) = 0 mod q.
3. Алиса выбирает e₁, q -тый
   корень которого был бы равен 1 mod p. Чтобы сделать это, Алиса выбирает примитивный элемент в Zp, e₀(см.
   “G. Список неприводимых и примитивных полиномов”
   ) и вычисляет e₁ = e₀^(p-1)/q mod p.
4. Алиса выбирает целое число, d, как свой секретный ключ.
5. Алиса вычисляет e₂ = e₁^d mod p.
6. Общедоступный ключ Алисы – (e_1, e₂, p, q), ее секретный ключ – (d).

В схеме цифровой подписи Шнорраобщедоступный ключ Алисы – (e1, e2, p, q) ; ее секретный ключ – (d).

Подписание и проверка

Рисунок 3.12 показывает схему цифровой подписи Шнорра.

Подписание

1. Алиса выбирает случайное число r. Обратите внимание, что открытый и секретный ключи могут использоваться для подписи многих сообщений. Но Алиса должна изменять r каждый раз,
   когда она передает новое сообщение. Обратите внимание также на то, что r должен иметь значение между 1 и q.
2. Алиса вычисляет первую подпись S₁ = h(M | e₁^r mod p) . Сообщение присоединяется (конкатенируется) спереди к значению e₁^r mod p, затем применяется хэш-функция, чтобы создать дайджест. Обратите внимание, что хэш-функция непосредственно не применяется к сообщению, но вместо этого она получается из последовательного соединения М. и e₁^r mod p.
3. Алиса вычисляет вторую подпись S₂ = r d x S₁ mod q. Обратите внимание, что эта часть – вычисление S₂ – делается в арифметике по модулю q.
4. Алиса передает М., S₁ и S₂.

Верификация (проверка) сообщения. Приемник, например Боб, получает М., S1 и S2.

1. Боб вычисляет V = h (М | e₁^S2 e₂^-S1 mod p).
2. Если S₂ конгруэнтно V по модулю p, сообщение принято; иначе оно отклоняется.

Пример 3.4

Вот тривиальный пример. Предположим, что мы выбираем q = 103 и p = 2267. Обратите внимание на то, что p = 22 x q 1. Мы выбираем e0 = 2, которое является элементом в Z2267*.

Мы выбираем d = 30, тогда e2 = 35430 mod 2267 = 1206. Секретный ключ Алисы -теперь – (d), ее общедоступный ключ – (e1,e2,p,q).

Алиса хочет передать сообщение М. Она выбирает r = 11 и вычисляет er = 35411 = 630 mod 2267. Предположим, что сообщение – 1000, и конкатенация (последовательное соединение) означает 1000630.

Также предположим, что хэширование этого значения дает дайджест h (1000630) = 200. Это означает S1 = 200. Алиса вычисляет S2 = r d x S1 mod q = 11 1026 200 mod 103 = 11 24 = 35.

Подделка по схеме подписи Шнорра

Похоже, что все атаки на схему Эль-Гамаля могут быть применены к схеме Шнорра. Однако схема Шнорра находится в лучшем положении, потому что S1 = h (М.

Схема цифровой подписи эллиптической кривой

Наша последняя схема – схема цифровой подписи эллиптической кривой(ECDSS – Elliptic Curve Digital Signature Scheme), которая основана на применении эллиптических кривых, – их мы обсуждали в

“B.

В процессе подписания две функции и экстрактор (извлекающее устройство) создают две подписи; в процессе проверки (верификации) обрабатывают выход одной функции (после прохождения через экстрактор) и сравнивают ее с первой подписью для проверки. Функции f1 и f3 фактически создают точки на кривой.

Первая создает новую точку для секретного ключа подписывающего лица. Вторая – новую точку из двух общедоступных ключей подписывающего лица. Каждый экстрактор извлекает первые координаты соответствующей точки в модульной арифметике. Детали входов и функций коротко обсуждаются далее.

Генерация ключей

Генерация ключей осуществляется следующими шагами:

1. Алиса выбирает эллиптическую кривуюEp (a,b) с
   простым числом p.
2. Алиса выбирает другое простое число q, чтобы использовать для вычисления.
3. Алиса выбирает секретный ключ d, целое число.
4. Алиса выбирает точку на кривой e₁(.,….)
5. Алиса вычисляет e₂ (..,….) = d x e₁ (……), другую точку на кривой.
6. Общедоступный ключ Алисы – (a, b, p, q, e₁, e₂), ее секретный ключ – d.

Подписание и проверка (верификация)

Рис. 3.16 показывает схему цифровой подписи эллиптической кривой.

Подписание. Процесс подписания состоит главным образом из выбора секретного случайного числа, создания третьей точки на кривой, вычисления двух подписей и передачи сообщения и подписей.

1. Алиса выбирает секретное случайное число, r, между 1 и q – 1.
2. Алиса выбирает третью точку на кривой, P (U, v) = r x e₁ (……).
3. Алиса использует первые координаты P (u, v), чтобы вычислить первую подпись S_1. Это означает S₁ = u mod q.
4. Алиса использует дайджест сообщения, свой секретный ключ и секретное случайное число r и S₁, чтобы вычислить вторую подпись S₂ = (h (M) d x S₁) r^-1 mod q,
5. Алиса передает М, S₁ и S₂.

Проверка (верификация).Процесс проверки состоит главным образом из восстановления третьей точки и подтверждения, что первая координата эквивалентна S1 по модулю q. Обратите внимание, что третья точка была создана подписывающим лицом, использующим секретное случайное число r.

1. Боб применяет М, S₁ и S₂ для создания двух промежуточных результатов A и B:

   A = h(M)S₂^-1 mod q

   B = S₂^-1S₁ mod q

   Затем Боб восстанавливает третью точку T(x,y) = A x e₁( … , …) B x e₂( … , …)

2. Боб использует первую координату из T(x,y), чтобы проверить сообщение. Если x = S₁ mod q, подпись принимается, иначе – отклоняется.

Схема цифровой подписи эль-гамаля

Криптосистема Эль-Гамаля была обсуждена в
“B. Стандарты и организации по стандартизации”
. Схема цифровой подписи Эль-Гамаля использует те же самые ключи, но алгоритм различен.
рис. 3.9 дает общую идею схемы цифровой подписи Эль-Гамаля.

В процессе подписания две функции создают две подписи. На стороне подтверждения обрабатывают выходы двух функций и сравнивают между собой для проверки. Обратите внимание, что одна и та же функция применяется и для подписания, и для проверки, но использует различные входы.

Рисунок показывает входы каждой функции. Сообщение – часть входа, для обеспечения функционирования при подписании; оно же – часть входа к функции 1 при подтверждении. Обратите внимание, что вычисления в функциях 1 и 3 проводятся по модулю p, а функции 2 – по модулю p – 1.

Генерация ключей

Процедура генерации ключей здесь точно такая же, как та, которая используется в криптографической системе. Выберем достаточно большое простое число p, чтобы в поле Z p* проблема дискретного логарифма была достаточно трудной.

Пусть e1 – простой элемент в Z p*. Алиса выбирает свой секретный ключ d, чтобы он был меньше, чем p – 1. Она вычисляет e2 = e1d.

Всхеме цифровой подписи Эль-Гамаля(e1, e2, p)- открытый ключ Алисы; d-секретный ключ Алисы.

Подтверждение и проверка

Рисунок 3.10 показывает схему цифровой подписи Эль-Гамаля.

Подписывающаяся Алиса может подписать дайджест сообщения, направленный к любому объекту, включая Боба.

1. Алиса выбирает секретное случайное число r. Обратите внимание, что хотя открытые и секретные ключи могут использоваться неоднократно, Алиса каждый раз нуждается в новом r, когда она подписывает новое сообщение.
2. Алиса вычисляет первую подпись S₁ = e^r mod p.
3. Алиса вычисляет вторую подпись S₂ = (М – d x S₁) x r^-1 mod (p – 1),где r – мультипликативная инверсия r по модулю p – 1.
4. Алиса передает М, S₁ и S₂ Бобу.

Проверка. Объект, например Боб, получает М, S1 и S2 и может проверить их следующим образом.

1. Боб проверяет, что 0 < S₁ < p.
2. Боб проверяет, что 0 < S₂ < p – 1.
3. Боб вычисляет V₁ = e₁^M mod p.
4. Боб вычисляет V₂ = e₂^S1 x e₂^S2 mod p.
5. Если V₁ является конгруэнтным V₂, сообщение принято; иначе оно будет отклонено. Мы можем доказать правильность этого критерия проверки, используя e₂ = e₁^d и S₁ = e₁^r:

   

   Мы имеем

   Поскольку e₁ – первообразный корень, может быть доказано, что вышеупомянутое сравнение справедливо тогда и только тогда, когда , и результат сравнения есть тот же самый S₂, с которого мы начали процесс подписания.

Пример 3.2

Ниже приводится тривиальный пример. Алиса выбрала p = 3119, e1 = 2, d = 127 и вычислила e2 = 2127 mod 3119 = 1702.

Она выбрала r равным 307. Она объявила e1, e2 и p ; она сохранила в тайне d. Далее показано, как Алиса может подписать сообщение.

Алиса передает М, S1 и S2 Бобу. Боб использует открытый ключ, чтобы вычислить, что сообщение подписано Алисой, потому что никто, кроме Алисы, не имеет секретного ключа d.

Поскольку V1 и V2 являются конгруэнтными, Боб принимает сообщение, и он предполагает, что сообщение было подписано Алисой, потому что никто, кроме нее, не имеет секретного ключа Алисы d.

Пример 3.3

Теперь вообразите, что Алиса хочет передать другое сообщение, М = 3000, Тэду. Она выбирает новое r = 107. Алиса передает М., S1 и S2 Тэду.

Поскольку V1 и V2 являются конгруэнтными, Тэд принимает сообщение; он предполагает, что сообщение подписано Алисой, потому что никто, кроме нее, не имеет секретного ключа Алисы d.

Подделка цифровой подписи в схеме Эль-Гамаля

Схема цифровой подписи Эль-Гамаля уязвима к экзистенциальной подделке, но селективную подделку на этой схеме сделать очень трудно.

Подделка только ключа. В этом типе подделки Ева имеет доступ только к открытому ключу. Возможны два варианта:

1. Ева имеет заранее заданное сообщение М. Она должна подделать подпись Алисы на этом сообщении. Ева должна найти две правильных подписи S₁ и S₂ для этого сообщения. Это – селективная подделка.
2. Ева может методом случайного подбора найти три значения, М, S₁ и S₂, такие, что подпись первого используется для второго. Если Ева может найти два новых параметра x и y, такие, что М = xS₂ mod (p – 1) и S₁ = -y S₂ mod (p – 1), то она может подделать сообщение, но серьезной выгоды не получит, поскольку это – экзистенциальная подделка.

Подделка при известном сообщении. Если Ева перехватила сообщение М и его две подписи S1 и S2, она может найти другое сообщение М’, с той же самой парой подписей S1 и S2. Однако обратите внимание, что это – экзистенциальная подделка, которая не помогает Еве.

Упражнения

1. Используя схему RSA, при p = 809, q = 751, и d = 23, вычислите общедоступный ключ e.

   Затем

2. Используя схему Эль-Гамаля при p = 881 и d = 700, найдите значения e₁ и e₂. Выберите r = 17. Найдите значение S₁ и S₂, если М = 400.
3. Используя схему Шнорра, при q = 83, p = 997 и d = 23, найдите значения для e₁ и e₂. Выберите r = 11. Если М
   = 400 и h (400) = 100, найдите значение S₁., S₂ и V. Равно ли ?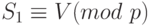
4. Используя схему DSS, при q = 59, p = 709 и d = 14, найдите значения для e₁ и e₂. Выберите r = 13. Найдите значение S₁ и S₂, если h (M) = 100. Проверьте подпись.
5. Сделайте следующее:
6. NIST-спецификация требует для DSS следующее: если значение S₂ = 0, то две подписи должны быть повторно вычислены, используя новый r. Какова причина этого?
7. Что случится, если Ева найдет значение r, используемое подписывающим лицом? Возможно ли это в принципе? Объясните ваш ответ отдельно для схем Эль-Гамаля-Шнорра, DSS.
8. Что случится, если Алиса подпишет два сообщения, используя одно и то же значение n? Объясните ваш ответ отдельно для каждого протокола: Эль-Гамаля, Шнорра или DSS.
9. Покажите пример уязвимости схемы RSA к селективной подделке, когда значения p и q являются маленькими. Используйте p = 19 и q = 3.
10. Покажите пример уязвимости схемы Эль-Гамаля к селективной подделке, когда значение p мало. Используйте p = 19.
11. Покажите пример уязвимости схемы Шнорра к селективной подделке, когда значения p и q являются маленькими. Используйте p =29 и q = 7.
12. Покажите пример уязвимости DSS к селективной подделке, когда значения p и q являются маленькими. Используйте p =29 и q = 7.
13. В схеме Эль-Гамаля, если Ева может найти значение r, может ли она подделать сообщение? Объясните.
14. В схеме Шнорра, если Ева может найти значение r, может ли она подделать сообщение? Объясните.
15. В DSS-схеме, если Ева может найти значение r, может ли она подделать сообщение? Объясните.
16. Предположим, что значения p, q, e₁ и r в схеме Шнорра – те же самые, что и соответствующие значения в DSS-схеме. Сравните значения S₁ и S₂ в схеме Шнорра с соответствующими значениями в DSS-схеме.
17. Объясните, почему в схеме Эль-Гамаля вычисление S₂ делается по модулю p, а вычисление S₂ делается по модулю p – 1.
18. Объясните, почему в схеме Шнорра вычисление S₁ делается по модулю p, а вычисление S₂ делается по модулю q.
19. Объясните, почему в схеме DSS вычисление S₁ делается по модулю p и модулю q, а вычисление S₂ делается только по модулю q.
20. В схеме Шнорра докажите правильность процесса проверки.
21. В DSS-схеме докажите правильность процесса проверки.
22. В схеме цифровой подписи эллиптической кривой докажите правильность процесса проверки.
23. Напишите два алгоритма для схемы RSА: один для процесса подписания и один для процесса проверки.
24. Напишите два алгоритма для схемы Эль-Гамаля: один для процесса подписания и один для процесса проверки.
25. Напишите два алгоритма для схемы Шнорра: один для процесса подписания и один для процесса проверки.
26. Напишите два алгоритма для DSS-схемы: один для процесса подписания и один для процесса проверки.
27. Напишите два алгоритма для схемы эллиптической кривой: один для процесса подписания и один для процесса проверки.

Шифрование

Сообщение M{displaystyle M} должно быть меньше числа p{displaystyle p}. Сообщение шифруется следующим образом:

1. Выбирается сессионный ключ — случайное целое число, взаимно простое с (p−1){displaystyle (p-1)}, k{displaystyle k} такое, что 1<k<p−1{displaystyle 1<k<p-1}.
2. Вычисляются числа a=gkmodp{displaystyle a=g^{k}{bmod {p}}} и b=ykMmodp{displaystyle b=y^{k}M{bmod {p}}}.
3. Пара чисел (a,b){displaystyle (a,b)} является шифротекстом.

Нетрудно заметить, что длина шифротекста в схеме Эль-Гамаля вдвое больше исходного сообщения M{displaystyle M}.