- Введение
- Что такое шифрование
- Difference between rsa algorithm and dsa – geeksforgeeks
- Асимметричные криптосистемы
- В чем разница между ключами rsa, dsa и ecdsa, которые использует ssh?
- Источники
- Как оно устроено
- Криптостойкость
- Надежность асимметричного шифрования
- Особенности асимметричного шифрования
- Особенности симметричного шифрования
- Подпись документов
- Получаем подпись сообщения
- Симметричное шифрование – как выглядит?
- Симметричные алгоритмы
- Сравнение криптостойкости некоторых систем шифрования
- Схема эль-гамаля
- Теорминимум
- Теперь к математике
- Шифруем, дешифруем…
- Экспертная оценка асимметричных криптоалгоритмов по методу саати
- Заключение
Введение
Наверняка вы сталкивались с таким понятием, как “электронная подпись”. Если обратиться к федеральному закону, то можно найти следующее её определение:
«Электронная подпись – информация в электронной форме, которая присоединена к другой информации в электронной форме (подписываемой информации) или иным образом связана с такой информацией и которая используется для определения лица, подписывающего информацию»
Для меня, как для человека, редко работающего с подобного рода документами, определение несколько абстрактное, хоть и отражает суть ЭП – определение лица, подписавшего некоторый документ. Помимо этого, ЭП может быть использована для определения искажений переданного сообщения, в чём мы сможем убедиться позднее.
Задача ЭП ясна, теперь хотелось бы увидеть и прочувствовать, что именно скрывается за этими двумя словами. Копаясь дальше в гугле, можно найти довольно много различных алгоритмов создания цифровой подписи (DSA, ГОСТ Р 34.10-2021, RSA-PSS и т.д.), разбираться в которых неподготовленному пользователю сложно.
Спасти эту ситуацию и помочь разобраться в том, что есть ЭП, может криптосистема RSA, разработанная Ривестом, Шамиром и Адлеманом в 1978 году. Она не загромождена безумным количеством алгоритмов и основывается на относительно простой математике. В связи с этим можно шаг за шагом прийти от модульной арифметики к алгоритму создания электронной подписи, чему я и хочу посвятить данную статью.
Что такое шифрование
Шифрование будет полезно тогда, когда нужно скрыть некоторую информацию от посторонних лиц и предоставить секретные данные авторизованным пользователям.
Особенностью такого вида передачи данных является использование ключа.
Есть три состояния безопасности:
- скрытие информации от посторонних;
- предотвращение изменений;
- сохранение целостности информации;
- идентификация отправителя.
Для чтения информации, кроме ключа, требуется дешифратор. Именно это обеспечивает невозможность получения данных злоумышленниками, ведь перехватив данные, но не имея ключа, прочесть их невозможно.
Бывают два вида шифрования: симметричный и асимметричный.
Главной целью шифрования является хранение информации. Это позволяет работать с некоторыми данными из ненадежных источников, передавать сообщения по незащищенным каналам. Отправка информации происходит так:
- отправитель шифрует данные;
- получатель расшифровывает.
Каждое преобразование реализуется с помощью алгоритмов, для решения которых используются ключи. Симметричные и асимметричные методы шифрования отличаются криптостойкостью.
Difference between rsa algorithm and dsa – geeksforgeeks
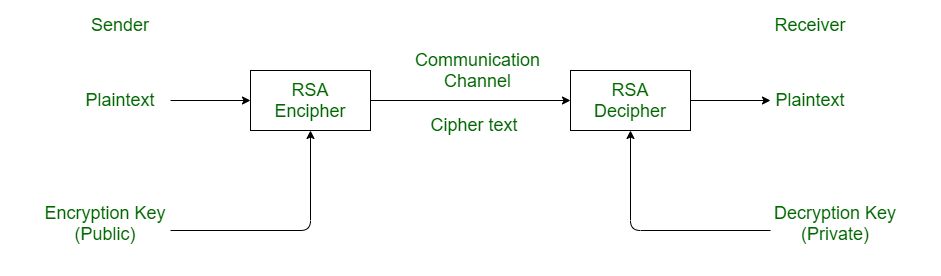
1. Rivest-Shamir-Adleman (RSA) algorithm :
RSA stands for Rivest-Shamir-Adleman. It is a cryptosystem used for secure data transmission. In RSA algorithm, encryption key is public but decryption key is private. This algorithm is based on mathematical fact that factoring the product of two large prime numbers is not easy. It was developed by Ron Rivest, Adi Shamir and Leonard Adleman in 1977.
Attention reader! Don’t stop learning now. Practice GATE exam well before the actual exam with the subject-wise and overall quizzes available in GATE Test Series Course.
Learn all GATE CS concepts with Free Live Classes on our youtube channel.
2. Digital Signature Algorithm (DSA) :
DSA stand for Digital Signature Algorithm. It is used for digital signature and its verification. It is based on mathematical concept of modular exponentiation and discrete logarithm. It was developed by National Institute of Standards and Technology (NIST) in 1991.
It involves four operations:
- Key Generation
- Key Distribution
- Signing
- Signature Verification
Difference between RSA algorithm and DSA :
| RSA | DSA |
|---|---|
| It is a cryptosystem algorithm. | It is digital signature algorithm. |
| It is used for secure data transmission. | It is used for digital signature and its verification. |
| It was developed in 1977. | While it was developed in 1991. |
| It was developed by Ron Rivest, Adi Shamir and Leonard Adleman. | It was developed by National Institute of Standards and Technology (NIST). |
| It uses mathematical concept of factorization of product of two large primes. | It uses modular exponentiation and discrete logarithm. |
| It is slower in key generation. | While it is faster in key generation as compared to RSA. |
| It in faster than DSA in encryption. | While it is slower in encryption. |
| It is slower in decryption. | While it is faster in decryption. |
| It is best suited for verification and encryption. | It is best suited for signing in and decryption. |
Асимметричные криптосистемы
Рассмотрим задачу сохранности содержимого посылки при передаче от отправителя к адресату. Вот картинка с многим полюбившимся Алисой и Бобом:
Алиса хочет передать Бобу посылку. Для начала Боб на своей стороне создает уникальные замок и ключ к нему (открытый и закрытый ключ соответственно). Далее, Боб делится с окружающим миром своим замком, чтобы любой желающий отправить ему посылку смог её закрыть.
Поскольку ключ от подобного замка один и находится только у Боба, никто, кроме Боба, просмотреть содержимое после защёлкивания замка не сможет. В конце концов, Алиса с помощью полученного замка закрывает посылку и передаёт Бобу, который открывает её своим ключом. Таким образом устроены асимметричные криптографические системы, которой как раз является RSA.
В схеме передачи посылки все объекты вполне материальны. Однако сообщения, которые мы хотим шифровать, являются ничем иным, как последовательностью бит, которую нельзя “закрыть” на физический замок. Таким образом возникают вопросы: что такое ключ и замок?
В чем разница между ключами rsa, dsa и ecdsa, которые использует ssh?
Вам все они нужны?
Нет, вашему ssh-серверу нужен только один, а клиенту нужно только поддерживать этот тип ключа для ssh-соединений.
RSA, DSA, ECDSA, EdDSA и Ed25519 все используются для цифровой подписи, но только RSA также может использоваться для шифрования.
RSA ( Rivest-Shamir-Adleman ) является одной из первых криптосистем с открытым ключом и широко используется для безопасной передачи данных. Его безопасность зависит от целочисленной факторизации , поэтому безопасный RNG (генератор случайных чисел) никогда не нужен. По сравнению с DSA RSA быстрее для проверки подписи, но медленнее для генерации.
DSA ( алгоритм цифровой подписи ) является федеральным стандартом обработки информации для цифровых подписей. Это безопасность зависит от дискретной логарифмической проблемы. По сравнению с RSA DSA быстрее для генерации подписи, но медленнее для проверки. Безопасность может быть нарушена, если используются плохие генераторы чисел .
ECDSA ( алгоритм цифровой подписи эллиптической кривой ) является реализацией алгоритма цифровой подписи DSA (эллиптической кривой). Криптография с эллиптической кривой способна обеспечить относительно тот же уровень безопасности, что и RSA, с меньшим ключом. Это также разделяет недостаток DSA в том, что он чувствителен к плохим RNG.
EdDSA ( алгоритм цифровой подписи с кривой Эдвардса ) представляет собой схему цифровой подписи, использующую вариант подписи Шнорра на основе кривых скрученных Эдвардса . Создание подписи является детерминированным в EdDSA, и ее безопасность основана на неразрешимости некоторых дискретных логарифмических проблем, поэтому она более безопасна, чем DSA и ECDSA, которая требует высокого качества случайности для каждой подписи.
Ed25519 , схема подписи EdDSA, но с использованием SHA-512/256 и Curve25519 ; это безопасная эллиптическая кривая, которая обеспечивает лучшую безопасность, чем DSA, ECDSA и EdDSA, плюс имеет лучшую производительность (не заметно для человека).
Другие примечания
Наиболее широко используются ключи RSA, поэтому они лучше всего поддерживаются.
ECDSA, (представленный в OpenSSH v5.7 ), вычислительно легче, чем DSA, но разница не заметна, если у вас нет машины с очень низкой вычислительной мощностью.
Начиная с OpenSSH 7.0 , SSH больше не поддерживает ключи DSA (ssh-dss) по умолчанию. Ключ DSA используется везде, согласно стандарту SSH (RFC 4251 и последующие).
Ed25519 был представлен в openSSH 6.5 .
Источники
Handbook of Applied Cryptography by A. Menezes, P. van Oorschot and S. Vanstone
Криптографические методы защиты информации: учеб. пособие / С. М. Владимиров, Э. М. Габидулин, А. И. Колыбельников, А. С. Кшевецкий; под ред. А. В. Уривского. – М.: МФТИ, 2021
Маховенко Е. Б. Теоретико-числовые методы в криптографии — М.: Гелиос АРВ, 2006.
NIST Special Publication 800-57 Part 3 Revision 1
Молдовян Н.А. Теоретический минимум и алгоритмы цифровой подписи. – СПб.: БХВ-Петербург, 2021. – Учебное пособие
Как оно устроено
Прежде, чем окунуться в необъятный мир математики рассмотреть, как именно устроена RSA, обратимся к тому, как работают
Криптостойкость
Симметричные и асимметричные системы шифрования имеют такую характеристику, которая отвечает за сложность получения несанкционированного доступа.
Существует 2 основных типа криптостойкости системы шифрования.
- Абсолютно стойкая система не может быть раскрыта, даже при наличии бесконечно больших вычислительных ресурсов. Характеризуется тем, что для каждого сообщения генерируется свой отдельный ключ. Его длина равна или больше длины сообщения.
- Достаточно стойкие системы применяются в криптографической системе гражданского назначения. Такой алгоритм сложно расшифровать, но при наличии соответствующих ресурсов это становится возможным.
Надежность асимметричного шифрования
Теоретически приватный ключ от асимметричного шифра можно вычислить, зная публичный ключ и механизм, лежащий в основе алгоритма шифрования (последнее — открытая информация). Надежными считаются шифры, для которых это нецелесообразно с практической точки зрения.
При этом фактическая надежность шифрования зависит в основном от длины ключа и сложности решения задачи, лежащей в основе алгоритма шифрования, для существующих технологий. Поскольку производительность вычислительных машин постоянно растет, длину ключей необходимо время от времени увеличивать.
Так, в 1977-м (год публикации алгоритма RSA) невозможной с практической точки зрения считалась расшифровка сообщения, закодированного с помощью ключа длиной 426 бит, а сейчас для шифрования этим методом используются ключи от 1024 до 4096 бит, причем первые уже переходят в категорию ненадежных.
Что касается эффективности поиска ключа, то она незначительно меняется с течением времени, но может скачкообразно увеличиться с появлением кардинально новых технологий (например, квантовых компьютеров). В этом случае может потребоваться поиск альтернативных подходов к шифрованию.
Особенности асимметричного шифрования
Применение пары открытый-закрытый ключ можно использовать как:
- самостоятельное средство защиты информации;
- средство распределения ключей;
- средства аутентификации пользователей.
Имеет такие преимущества:
- сохранение секретного ключа в надежном месте, вместо которого по открытому каналу передается открытый;
- ключ дешифрования известен только одной стороне;
- в большой асимметричной системе используйте меньшее количество ключей в отличие от симметричной.
В таких алгоритмах сложно внести какие-либо изменения. Подобная система имеет длинные ключи. Если симметричный ключ имеет размер 128 Бит, то ключ RSA – 2304 Бит. Из-за этого страдает скорость расшифровывания – она в 2-3 раза медленнее. Для расшифровки требуются большие вычислительные ресурсы.
Существует очень много примеров симметричной и асимметричной систем шифрования.
Особенности симметричного шифрования
Симметричная система защита имеет следующие достоинства.
- Высокая скорость и простота реализации.
- Для обеспечения стойкости шифра используется малая длина ключа.
К недостаткам относится следующее:
- сложность управления ключами в большой сети;
- сложность обмена ключами;
- потребность в поиске надежного канала для передачи ключа сторонам;
- невозможность использования для цифровой подписи, сертификатов.
Для компенсации недостатков используется комбинированная схема, в которой с помощью асимметричного шифрования передается ключ, используемый для дешифровки. Он передается при помощи симметричного шифрования.
Подпись документов
Рассмотренный алгоритм получения подписи изящен и прост в осознании, однако операция возведения в степень несколько “мешается”. Наша текущая задача – подписать объёмный документ. Чтобы сэкономить время, мы не будем подписывать содержимое документа, а прибегнем к помощи хэш-функций (если вы не знаете, что такое хэш-функция, рекомендую почитать википедию).
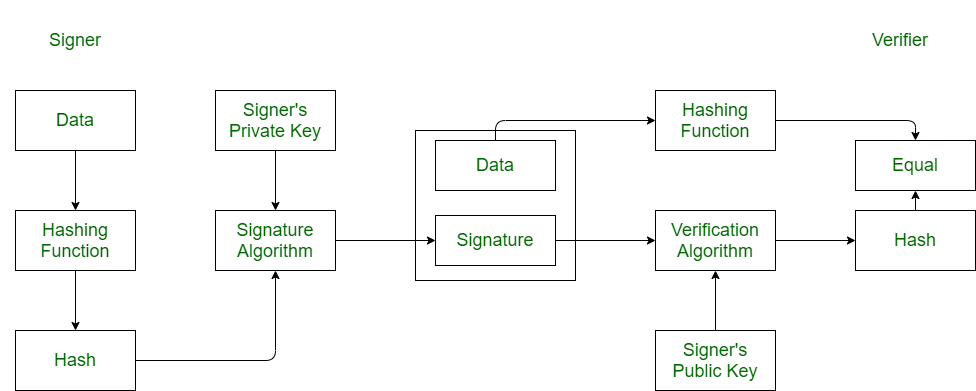
На картинках наглядно показано, в какой момент мы используем хэширование. Создание подписи:
Проверка подписи:
В качестве хэш-функции можно использовать SHA-256, как это сделано, например, в PGP. По теме практического создания электронной подписи с использованием PGP на хабре уже написана статья, поэтому на этом месте имеет смысл поставить точку и перейти к заключению.
Получаем подпись сообщения
Ещё раз напишем две ключевые формулы шифрования и расшифрования соответственно:
Теперь давайте предположим, что Боб хочет отправить Алисе открытку m от своего имени. У Боба в распоряжении уже имеются два ключа (e, n) и d, которые он сгенерировал по алгоритму, описанному ранее. Поскольку d является закрытым ключом, то можно им воспользоваться как уникальным идентификатором Боба. Давайте “зашифруем” m с помощью d:
Результат данной операции и есть подпись сообщения Боба. Заметим, что подпись напрямую зависит от подписываемого сообщения, а не только от того, что его подписывает Боб. Далее, Алиса получает сообщение m, подпись s и открытый ключ (e, n).
Если Алиса получила, что m ≡ m′, то подпись считается правильной.
Дочитавших до этого места хочу поздравить с получением первой цифровой подписи “на бумаге”!
Симметричное шифрование – как выглядит?
Пример симметричного шифрования и схема реализации ниже.
- Есть два собеседника, которые планируют обменяться конфиденциальной информацией.
- Первый собеседник генерирует ключ d, алгоритмы шифрования E и дешифрования D. Затем посылает эту информацию второму собеседнику.
- Сообщение дешифруется ключом d.
Главным недостатком является невозможность установить подлинность текста. В случае перехвата ключа злоумышленник расшифрует секретную информацию.
Существуют классические методы.
- Простая и двойная перестановка.
- Магический квадрат.
- Одиночная перестановка.
Первый метод является одним из простейших, в схеме которого не используется ключ. Отправитель и получатель договариваются о некотором ключе, представленным в виде размера таблицы. Передаваемое сообщение записывается в столбцы таблицы, но считывается по строкам. Зная размер таблицы, получатель расшифровывает сообщение.
Для обеспечения большей скрытности используется двойная перестановка. Таким образом происходит шифрование ранее зашифрованного текста. Для этого таблицы должны отличаться количеством строк и столбцов. Они заполняются вертикально, горизонтально, змейкой, по спирали. Этот способ не усиливает шифрование, но процесс взлома становится более длительным.
“Магический квадрат” – более сложная структура, которая представляет собой матрицу. В клетки вписываются натуральные числа таким образом, чтобы сумма чисел по каждому столбцу, строке, диагонали была одинаковой. Каждое число соответствует букве сообщения. Полученный текст выписывается в строку, сопоставляя числа и символы.
Симметричные алгоритмы
Один и тот же «ключ» используется для шифрования и дешифрования файла. Они подразделяются на потоковые и блочные шифры. Потоковый шифр – цифры открытого текста объединяются с потоком псевдослучайных цифр шифра. Блочные шифры берут количество битов и шифруют их как единое целое.
Сам алгоритм не держится в секрете, и отправитель и получатель сообщения должны иметь копии секретного ключа в надежном месте. Использование одного и того же ключа также является одним из недостатков криптографии с симметричным ключом, поскольку, если кто-то может получить ключ, он может расшифровать ваши данные.
Data Encryption Standard – DESСтандарт шифрования данных DES является одним из наиболее известных алгоритмов современной криптографической эры. DES был разработан в 1970-х годах IBM и позже был представлен Национальному бюро стандартов (NBS)
Сегодня DES считается небезопасным. DES и double-DES больше не используются, но тройной DES с тремя ключами все еще является рекомендуемым алгоритмом в NIST SP 800-57 . DES намного медленнее, чем алгоритм AES, но все еще встречается в индустрии электронных платежей .
Advanced Encryption Standard – AESРасширенный стандарт шифрования AES был установлен Национальным институтом стандартов и технологий (NIST) в 2001 году. AES был принят правительством США с длинами ключей 128, 192 и 256 бит.
Сегодня AES по прежнему широко используется для повышения вычислительной мощности и возможности использования в широком спектре аппаратного обеспечения, таких как смарт-карты и высокопроизводительные компьютеры.
Advanced Encryption Standard Proces – MARSMARS разработан коллективом криптологов из корпорации IBM, он поддерживает 128-битные блоки и ключи переменного размера на нескольких основных и смешанных раундах, обеспечивая сильное сопротивление криптографической атаке.
International Data Encryption Algorithm – IDEAМеждународный алгоритм шифрования данных (IDEA), первоначально называвшийся Improved Proposed Encryption Standard (IPES) впервые обсуждался в 1991 году. IDEA был незначительный пересмотр предлагаемого стандарта шифрования (PES), предназначенного в качестве замены DES.
Сегодня широко не используется, не имеет патентов и полностью бесплатна для любого использования, но само название все еще является торговой маркой. Он работал на 64-битном блоке с использованием 128-битного ключа и все еще является необязательным алгоритмом в стандарте OpenPGP
RC 2Шифр Ривеста, код Рона или алгоритмы RC, были изобретены Роном Ривестом в 1987 году.
Сегодня не рекомендуется для использования. Он уязвим для атаки.
RC 4Шифр был разработан Роном Ривестом в 1987 году и в 1994 году был быстро взломан. Алгоритм никогда не был официально признан RSA Security, но он использовался в некоторых протоколах и стандартах шифрования
Сегодня не рекомендуется для использования.
RC 5Шифр разработан Роном Ривестом и его коллегами в 1994 году
Сегодня не рекомендуется для использования.
RC 6Шифр был получен из RC5 Роном Ривестом и его коллегами.
BlowfishСимметричный блочный шифр, созданный Брюсом Шнайером в качестве замены DES и IDEA.
TwofishШифр Twofish является преемником Blowfish, опубликован в 1998 году.
ThreefishШифр был создан в 2008 году
Сегодня используется без патента
SerpentШифр разработан в 1998 году Россом Андерсоном, Эли Бухамом и Ларсом Кнудсеном.
Сегодня используется без патента
Сравнение криптостойкости некоторых систем шифрования
Максимальный размер ключа RSA – 4096 бит.
Он используется для шифрования и подписи. Криптостойкость можно описать как 2,7•1028 для ключа 1300 Бит. Схема применяется во многих стандартах, принцип шифрования RSA один из первых асимметричных алгоритмов.
Размер ключа схемы Эль-Гамаля равен RSA – 4096 Бит. Он используется и для шифрования, и для цифровой подписи. Криптостойкость этой системы не отличается от RSA при одинаковом размере ключа.
В методе DSA используется значительно меньшей ключ – 1024 бита. Применяется он исключительно для цифровой подписи.
Схема эль-гамаля
Шифрование по схеме Эль-Гамаля используется для цифровых подписей. Является продолжением алгоритма Диффи-Хеллмана.
При работе по этой схеме важно учитывать следующую особенность. Шифрование Эль-Гамаля не является алгоритмом цифровой подписи по схеме с одноименным названием. При шифровке текст преобразовывается в шифр, который длиннее исходного сообщения в 2 раза.
Генерация ключей происходит следующим образом.
- Выбирается случайное простое число p.
- Число g должно быть первообразным корнем p.
- Число x должно быть больше 1 и меньше p-1. Это будет закрытый ключ.
- Затем вычисляется открытый ключ y по формуле
g^x mod p.
При шифровании текста M выбирается системный ключ K. Он больше единицы и меньше p-1. Затем вычисляются числа a и b, которые являются шифротекстом, a = g^k mod p и b = y^k M mod p.
Теорминимум

Сформируем небольшой словарик терминов, которые нам пригодятся далее:
Хочу отметить, что на данном этапе подразумевается, что вы знакомы с арифметическими операциями по модулю. Если нет, то здесь можно о них почитать.
Теперь к математике
Асимметричные криптографические системы основаны на так называемых односторонних функциях с секретом. Под односторонней понимается такая функция я y=f(x), которая легко вычисляется при имеющемся x, но аргумент x при заданном значении функции вычислить сложно.
Аналогично, односторонней функцией с секретом называется функция y=f(x, k), которая легко вычисляется при заданном x, причём при заданном секрете k аргумент x по заданному y восстановить просто, а при неизвестном k – сложно.
Подобным свойством обладает операция возведения числа в степень по модулю:
Здесь φ(n) – функция Эйлера числа n. Пока условимся, что это работает, далее это будет доказано более строго. Теперь нужно понять, что из это является ключами Боба, а что сообщением. В нашем распоряжении имеются числа c, m, n, e, d.
Давайте посмотрим на первое выражение. Здесь число c получено в результате возведения в степень по модулю числа m. Назовём это действие шифрованием. Тогда становится очевидно, что m выступает в роли открытого текста, а c – шифртекста.
Результат c зависит от степени e, в которую мы возводим m, и от модуля n, по которому мы получаем результат шифрования. Эту пару чисел (e, n) мы будем называть открытым ключом. Им Алиса будет шифровать сообщение.
Смотрим на второе действие. Здесь d является параметром, с помощью которого мы получаем исходный текст m из шифртекста c. Этот параметр мы назовём закрытым ключом и выдадим его Бобу, чтобы он смог расшифровать сообщение Алисы.
Что есть что разобрались, теперь перейдём к конкретике, а именно – генерации ключей Боба. Давайте выберем число n такое, что:
где p и q – некоторые разные простые числа. Для такого n функция Эйлера имеет вид:
Такой выбор n обусловлен следующим. Как вы могли заметить ранее, закрытый ключ d можно получить, зная открытый e. Зная числа p и q, вычислить функцию Эйлера не является вычислительно сложной задачей, ровно как и нахождение обратного элемента по модулю.
Однако в открытом ключе указано именно число n. Таким образом, чтобы вычислить значение функции Эйлера от n (а затем получить закрытый ключ), необходимо решить задачу факторизации, которая является вычислительно сложной задачей для больших n (в современных системах, основанных на RSA, n имеет длину 2048 бит).
Возвращаемся к генерации ключей. Выберем целое число e:
Для него вычислим число d:
Для отыскания числа, обратного по модулю, можно воспользоваться алгоритмом Евклида.
Мы завершили с этапом генерации ключей. Теперь Боб публикует свой открытый ключ (e, n), прячет закрытый d, а мы переходим к Алисе.
Шифруем, дешифруем…
Возьмём в качестве сообщения число m (m ∈ [1, n − 1]). Чтобы Алисе зашифровать его, необходимо возвести его в степень e по модулю n. Эти числа идут вместе с открытым ключом Боба:
Здесь за с обозначен шифртекст, который Алиса будет должна передать Бобу. Отметим также, что c ∈ [1, n − 1], как и m. Расшифруем шифртекст, возведя его в степень закрытого ключа Боба d:
А теперь ответим на вопрос, почему m ≡ m′ . Ниже я приведу доказательство данного утверждения, но если оно (доказательство) вам не сильно интересно, то можете его пропустить и просто поверить, что это так.
Доказательство
Экспертная оценка асимметричных криптоалгоритмов по методу саати
В данной статье приводится сравнительный анализ пяти широко известных асимметричных криптоалгоритмов на основе актуальных критериев — показателей качества. В ходе исследования выясняются достоинства и недостатки рассматриваемых криптоалгоритмов, а также недостатки асимметричной системы шифрования в целом.
Нынешняя информационная эпоха, давшая человечеству инструментарий для существенного упрощения процесса общения и работы, также стала причиной появления множества актуальных на сегодняшний день проблем. Обеспечение целостности и должного уровня конфиденциальности передаваемой посредством сети Интернет информации является одной из самых важных проблем, и для её разрешения были разработаны различные симметричные и асимметричные криптоалгоритмы. В данной статье речь пойдёт об асимметричных криптоалгоритма. В результате анализа сферы защиты информации были выявлены следующие представители асимметричной криптографии:
- RSA;
- DSA;
- шифросистема Эль-Гамаля;
- обмен ключами Диффи—Хелмана;
- протокол Аншеля-Гольдфельда.
Основная цель данной работы заключается в процессе исследования перечисленных криптоалгоритмов и их экспертной оценке, построенной по заданным критериям качества.
Базой количественной оценки программ является не только аналитическо-иерархическая процедура Саати, повсеместно эксплуатируемая для точного определения весовых коэффициентов критериев качества. Помимо неё, также нашёл применение метод экспертных оценок, задачей которого является получение количественных значений критериев качества.
Для оценочного сравнения выбранных криптоалгоритмов проведём их сравнительный анализ посредством метода Саати [1]. Чуть ниже отображены выбранные критерии, на основании которых будет проводиться оценочная процедура:
А1 — Криптостойкость (MIPS);
А2 — Размер генерируемого ключа (до 4096 бит);
А3 — Назначение (шифрование и цифровая подпись);
А4 — Скорость шифрования (при длине модуля в 1024 бита);
А5 — Скорость дешифрования (при длине модуля в 1024 бита).
Используя аналитическо-иерархическую процедуру Саати, установим для каждого критерия качества его вес [2].
Правила заполнения матрицы парных сравнений представлены в таблице 1.
Таблица 1. Значения коэффициентов матрицы парных сравнений
Xij | Значение |
1 | i-ый критерий практически равноценен j-му |
3 | i-ый критерий в меньшей степени важнее j-го |
5 | i-ый критерий важнее j-го |
7 | i-ый критерий в большей степени важнее j-го |
9 | i-ый критерий намного важнее j-го |
Матрица парных сравнений, веса критериев и средние геометрические занесены в таблицу 2.
Таблица 2. Матрица парных сравнений, средние геометрические и веса критериев.
A1 | A2 | A3 | A4 | A5 | Среднее геометрическое | Веса критериев | |
A1 | 1 | 3/1 | 7/1 | 5/1 | 5/1 | 3,5 | 0,49 |
A2 | 1/3 | 1 | 5/1 | 5/1 | 5/1 | 2,11 | 0,29 |
A3 | 1/7 | 1/5 | 1 | 3/1 | 3/1 | 0,76 | 0,11 |
A4 | 1/5 | 1/5 | 1/3 | 1 | 1 | 0,42 | 0,06 |
A5 | 1/5 | 1/5 | 1/3 | 1 | 1 | 0,42 | 0,06 |
На рисунке 1 изображена созданная на основании данных таблицы 2 диаграмма весовых коэффициентов для критериев A1, A2, A3, A4 и A5.

Чтобы проверить матрицу парных сравнений на непротиворечивость, произведём её проверку. Суммы столбцов матрицы парных сравнений [3]:
R1=1.88; R2=4.6; R3=13.67; R4=15; R5=15.
После вычислим дополнительную величину L, просуммировав весовые коэффициенты и произведения сумм столбцов матриц: L = 5,45.
Таким образом, индекс согласованности ИС = (L-N)/(N-1) = 0,113.
Следовательно, величина случайной согласованности для размерности матрицы парных сравнений: СлС = 1,24.
Отношение согласованности ОС=ИС/СлС = 0,09 не превышает 0,2, а значит, дополнительное уточнение матрицы парных сравнений не требуется [4].
Используя вычисленные коэффициенты, найдём интегральный показатель качества для следующих асимметричных алгоритмов шифрования данных: RSA, DSA, шифросистема Эль-Гамаля, обмен ключами Диффи—Хелмана, протокол Аншеля—Гольдфельда.
Установим категориальную шкалу от нуля до семи (где 0 — качество не удовлетворительно, а 7 — предельно достижимый уровень качества) для установления функциональных возможностей выбранных криптоалгоритмов.
Значения весовых коэффициентов ai, соответствующие функциональным возможностям аналогов [5]:
- Криптостойкость (MIPS): a1 = 0.34;
- Размер генерируемого ключа (до 4096 бит): a2 = 0.24;
- Назначение (шифрование и цифровая подпись): a3 = 0.16;
- Скорость шифрования (при длине модуля в 1024 бита): a4 = 0.13;
- Скорость дешифрования (при длине модуля в 1024 бита): a5 = 0.13;
где  [6]. По выбранной шкале определим количественные значения функциональных возможностей Xij (таблица 3) и вычислим интегральные показатели качества для выбранных асимметричных алгоритмов шифрования:
[6]. По выбранной шкале определим количественные значения функциональных возможностей Xij (таблица 3) и вычислим интегральные показатели качества для выбранных асимметричных алгоритмов шифрования:
Таблица 3. Интегральные показатели качества
Критерии | Весовые коэффициенты | Асимметричные алгоритмы | Базовые значения | ||||
RSA | DSA | шифросистема Эль-Гамаля | обмен ключами Диффи-Хелмана | протокол Аншеля- Гольдфельда | |||
Криптостойкость (MIPS) | 0,49 | 7 | 7 | 7 | 5 | 5 | 6,2 |
Размер генерируемого ключа (до 4096 бит) | 0,29 | 5 | 3 | 7 | 3 | 5 | 4,6 |
Назначение (шифрование и цифровая подпись) | 0,11 | 7 | 7 | 7 | 3 | 3 | 5,45 |
Скорость шифрования (при длине модуля в 1024 бита) | 0,06 | 7 | 7 | 3 | 5 | 3 | 4,95 |
Скорость дешифрования (при длине модуля в 1024 бита) | 0,06 | 3 | 3 | 7 | 3 | 3 | 3,8 |
Интегральные показатель качества Q | 6,25 | 5,67 | 6,83 | 4,13 | 4,59 | 5,49 | |
где  — интегральный показатель качества для j-го криптоалгоритма.
— интегральный показатель качества для j-го криптоалгоритма.
Построим лепестковую диаграмму интегрального показателя качества каждого криптоалгоритма (рисунок 2).
Значения характеристик функциональных возможностей (критериев) представлена в виде лепестковой диаграммы на рисунке 3.
Сравнительный анализ криптоалгоритмов с открытым ключом показал, что из всех представленных аналогов ни один не обладает максимально высокими показателями по всем заявленным параметрам, в особенности рассмотренные криптоалгоритмы страдают от низкой скорости шифрации и дешифрации передаваемых данных, которая обусловлена их классической асимметричной структурой [7]. Данная методика экспертной оценки асимметричных криптоалгоритмов позволила оценить их качество с позиции уровня реализуемых функций [8].
Заключение
Вот мы и прошли все стадии создания электронной подписи, начиная с простой модульной арифметики и заканчивая, собственно, получением подписи. Обладая этими знаниями, вы можете попробовать перевести их на ваш любимый язык программирования и написать свою защищенную аську, например. В том, как именно их применить, вас ограничит только ваше воображение.
Отмечу, что другие существующие алгоритмы создания ЭП основаны на схожих принципах, поэтому надеюсь, что после прочтения этой статьи вам будет проще разобраться в них. “Следующей по сложности” я обозначу криптосистему Эль-Гамаля, но о ней уже не в этом посте.
Спасибо за внимание!








