- Описание алгоритма rsa
- 001. криптография и цифровая подпись rsa-sha256 на платформе 1с
- Алгоритм подписания информации (документа)
- Генерация и отправка ключа серверу
- Защищённость
- Концепция алгоритма rsa
- Криптопровайдеры, инициализация и деинициализация
- Симметричные шифры des и 3des
- Симметричные шифры des, 3des, rijndael
- Создание и проверка эцп документа | блог о шифровании
- Структура и возможности
- Фрагменты кода
- Хеши md5 и sha
- Электронная цифровая подпись
Описание алгоритма rsa
RSA — криптографический алгоритм с открытым ключом. RSA стал первым алгоритмом такого типа, пригодным и для шифрования и для цифровой подписи. Алгоритм используется в большом числе криптографических приложений.
История
Описание RSA было опубликовано в 1977 году Рональдом Ривестом (Ronald Linn Rivest), Ади Шамиром (Adi Shamir) и Леонардом Адлеманом (Leonard Adleman) из Массачусетского Технологического Института (MIT).
Британский математик Клиффорд Кокс (Clifford Cocks), работавший в центре правительственной связи (GCHQ) Великобритании, описал аналогичную систему в 1973 году во внутренних документах центра, но эта работа не была раскрыта до 1977 года и Райвест, Шамир и Адлеман разработали RSA независимо от работы Кокса.
В 1983 году MIT был выдан патент 4405829 США, срок действия которого истёк 21 сентября 2000 года.
Описание алгоритма
Безопасность алгоритма RSA основана на трудности задачи разложения на множители. Алгоритм использует два ключа — открытый (public) и секретный (private), вместе открытый и соответствующий ему секретный ключи образуют пару ключей (keypair). Открытый ключ не требуется сохранять в тайне, он используется для зашифрования данных. Если сообщение было зашифровано открытым ключом, то расшифровать его можно только соответствующим секретным ключом.
Генерация ключей
Для того, чтобы сгенерировать пару ключей выполняются следующие действия:
1. Выбираются два больших простых числа ![]() и
и ![]() и
и 2. Вычисляется их произведение
![]() 3. Вычисляется Функция Эйлера
3. Вычисляется Функция Эйлера ![]() 3. Вычисляется Функция Эйлера
3. Вычисляется Функция Эйлера 4. Выбирается целое
![]() такое, что
такое, что ![]() такое, что
такое, что и
![]() взаимно простое с
взаимно простое с ![]() взаимно простое с
взаимно простое с 5. С помощью расширенного алгоритма Евклида находится число
![]() такое, что
такое, что ![]() такое, что
такое, что Число
![]() называется модулем, а числа
называется модулем, а числа ![]() называется модулем, а числа
называется модулем, а числа и
![]() — открытой и секретной экспонентами, соответственно. Пара чисел
— открытой и секретной экспонентами, соответственно. Пара чисел ![]() — открытой и секретной экспонентами, соответственно. Пара чисел
— открытой и секретной экспонентами, соответственно. Пара чисел является открытой частью ключа, а
![]() — секретной. Числа
— секретной. Числа ![]() — секретной. Числа
— секретной. Числа и
![]() после генерации пары ключей могут быть уничтожены, но ни в коем случае не должны быть раскрыты.
после генерации пары ключей могут быть уничтожены, но ни в коем случае не должны быть раскрыты.
Зашифрование и расшифрование
Для того, чтобы зашифровать сообщение ![]() вычисляетсяЧисло
вычисляетсяЧисло ![]() вычисляетсяЧисло
вычисляетсяЧисло и используется в качестве шифртекста. Для расшифрования нужно вычислить
Нетрудно убедиться, что при расшифровании мы восстановим исходное сообщение:
Из условия
следует, что
![]() для некоторого целого
для некоторого целого ![]() для некоторого целого
для некоторого целого , следовательно
Согласно теореме Эйлера:
поэтому
Некоторые особенности алгоритма
Генерация простых чисел
Для нахождения двух больших простых чисел ![]() и
и ![]() и
и , при генерации ключа, обычно используются вероятностные тесты чисел на простоту, которые позволяют быстро выявить и отбросить составные числа.Для генерации
![]() и
и ![]() и
и необходимо использовать криптографически надёжный генератор истинно случайных чисел. У нарушителя не должно быть возможности получить какую-либо информацию о значениях этих чисел.
![]() и
и ![]() и
и не должны быть слишком близки друг к другу, иначе можно будет их найти используя метод факторизации Ферма. Кроме того, необходимо выбирать «сильные» простые числа, чтобы нельзя было воспользоваться p-1 алгоритмом Полларда.
Дополнение сообщений
При практическом использовании необходимо некоторым образом дополнять сообщения. Отсутствие дополнений может привести к некоторым проблемам:
· значения ![]() и
и ![]() и
и дадут при зашифровании шифртексты 0 и 1 при любых значениях
![]() и
и ![]() и
и .· при малом значении открытого показателя (
![]() , например) возможна ситуация, когда окажется, что
, например) возможна ситуация, когда окажется, что ![]() , например) возможна ситуация, когда окажется, что
, например) возможна ситуация, когда окажется, что . Тогда
![]() , и нарушитель легко сможет восстановить исходное сообщение вычислив корень степени
, и нарушитель легко сможет восстановить исходное сообщение вычислив корень степени ![]() , и нарушитель легко сможет восстановить исходное сообщение вычислив корень степени
, и нарушитель легко сможет восстановить исходное сообщение вычислив корень степени из
![]() .
.
· поскольку RSA является детерминированным алгоритмом, т.е. не использует случайных значений в процессе работы, то нарушитель может использовать атаку с выбранным открытым текстом.
Для решения перечисленных проблем сообщения дополняются перед каждым зашифрованием некоторым случайным значением — солью. Дополнение выполняется таким образом, чтобы гарантировать, что ![]() ,
, ![]() ,
, и
![]() . Кроме того, поскольку сообщение дополняется случайными данными, то зашифровывая один и тот же открытый текст мы каждый раз будем получать другое значение шифртекста, что делает атаку с выбранным открытым текстом невозможной.
. Кроме того, поскольку сообщение дополняется случайными данными, то зашифровывая один и тот же открытый текст мы каждый раз будем получать другое значение шифртекста, что делает атаку с выбранным открытым текстом невозможной.
Выбор значения открытого показателя
RSA работает значительно медленнее симметричных алгоритмов. Для повышения скорости шифрования открытый показатель ![]() выбирается небольшим, обычно 3, 17 или 65537. Эти числа в двоичном виде содержат только по две единицы, что уменьшает число необходимых операций умножения при возведении в степень. Например, для возведения числа
выбирается небольшим, обычно 3, 17 или 65537. Эти числа в двоичном виде содержат только по две единицы, что уменьшает число необходимых операций умножения при возведении в степень. Например, для возведения числа ![]() выбирается небольшим, обычно 3, 17 или 65537. Эти числа в двоичном виде содержат только по две единицы, что уменьшает число необходимых операций умножения при возведении в степень. Например, для возведения числа
выбирается небольшим, обычно 3, 17 или 65537. Эти числа в двоичном виде содержат только по две единицы, что уменьшает число необходимых операций умножения при возведении в степень. Например, для возведения числа в степень 17 нужно выполнить только 5 операций умножения:
Выбор малого значения открытого показателя может приводить к раскрытию сообщения, если оно отправляется сразу нескольким получателям, но эта проблема решается за счёт дополнения сообщений.
Выбор значения секретного показателя
Значение секретного показателя ![]() должно быть достаточно большим. В 1990 году Михаэль Винер (Michael J. Wiener) показал, что если
должно быть достаточно большим. В 1990 году Михаэль Винер (Michael J. Wiener) показал, что если ![]() должно быть достаточно большим. В 1990 году Михаэль Винер (Michael J. Wiener) показал, что если
должно быть достаточно большим. В 1990 году Михаэль Винер (Michael J. Wiener) показал, что если и
![]() , то имеется эффективный способ вычислить
, то имеется эффективный способ вычислить ![]() , то имеется эффективный способ вычислить
, то имеется эффективный способ вычислить по
![]() и
и ![]() и
и . Однако, если значение
![]() выбирается небольшим, то
выбирается небольшим, то ![]() выбирается небольшим, то
выбирается небольшим, то оказывается достаточно большим и проблемы не возникает.
Длина ключа
Число n должно иметь размер не меньше 512 бит. В настоящий момент система шифрования на основе RSA считается надёжной, начиная с размера N в 1024 бита.
Применение RSA
Система RSA используется для защиты программного обеспечения и в схемах цифровой подписи. Также она используется в открытой системе шифрования PGP.
Из-за низкой скорости шифрования (около 30 кбит/с при 512 битном ключе на процессоре 2 ГГц), сообщения обычно шифруют с помощью более производительных симметричных алгоритмов со случайным ключом (сеансовый ключ), а с помощью RSA шифруют лишь этот ключ.
001. криптография и цифровая подпись rsa-sha256 на платформе 1с
Комплект программного обеспечения для реализации функций оптического распознавания штрих-кодов различных систем при помощи обычной web-камеры, а также их отображения в печатных формах. Программы могут работать в составе конфигураций, созданных на базе платформ «1С-Предприятие» версий 7.7, 8.2, 8.3. Компонент чтения кодов реализован в виде внешней компоненты 1С с COM-интерфейсом. Компонент отображения создан по стандартной технологии ActiveX для Windows, и может быть встроен в любое приложение, поддерживающее встраивание ActiveX элементов управления, например в документ Word или Excel, или форму VBA.
P.S. Добавлена новая версия программы распознавания. Новые функции: обработка видео в реальном режиме (а не по таймеру, как раньше), добавлена возможность распознавания штрих-кодов из графических файлов JPEG, PNG, GIF, BMP, а также передавать для распознавания картинки из 1С, теперь можно получить в 1С захваченное с камеры или файла изображение, как с выделением мест, содержащих коды, так и без, а также отдельные фрагменты изображений, содержащие код. Добавлены новые свойства и методы для программирования. Обновлена документация.
10 стартмани
10.07.2022
81870
94
igorberezhnov
121
Алгоритм подписания информации (документа)
Для создания подписи потребуется:
Поскольку асимметричные алгоритмы достаточно медленные по сравнению с симметричными, то объем подписываемых данных играет большую роль и если он велик, то обычно берут хэш от подписываемых данных, а не сами данные. Хэш получают с помощью хэш-функций, например, SHA512, которая принимает на вход некую информацию и возвращает хэш определенной длины.
Хэш-функция как мясорубка, можно прокрутить мясо и получить фарш, но обратно из фарша уже мясо не получишь. Таким образом, ЭЦП ставится не на сам документ, а на его хэш. Хэш-функции не являются частью алгоритма ЭЦП, поэтому в схеме может быть использована любая надёжная хэш-функция.
Этапы:
- С помощью RSA, генерируем пару публичный и приватный ключи;
- Подписываемые данные подставляем в функцию SHA512 и получаем хэш;
- Полученный хэш и закрытый ключ подставляем в функцию асимметричного шифрования RSA, то есть RSAEncode(хэш от информации, закрытый ключ), на выходе получим строку – ЭЦП.
Алгоритм подписи данных продемонстрирован на рисунке 2.
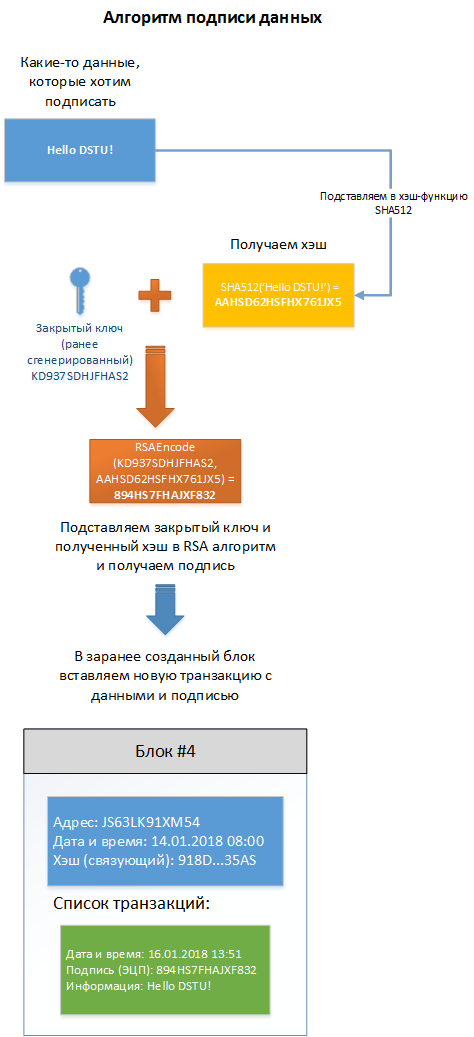 Рисунок 2 — алгоритм подписи данных
Рисунок 2 — алгоритм подписи данных
Генерация и отправка ключа серверу
В нашем проекте используется трехуровневая архитектура: клиент-сервер-база данных. Сервер написан на Java, клиент — на C#. Ниже я буду описывать реализацию шифрования как на серверной части, так и на клиентской. Начнем именно с пользователя — клиента.
Итак, соединение с сервером прошло успешно, и он готов принимать пакеты. Для этого мы создаем ключ, используя .NET класс RSACryptoServiceProvider (C#):
- private RSACryptoServiceProvider m_Rsa;
- private RSAParameters m_ExternKey;
- private RSAParameters m_InternKey;
- public CryptoRsa()
- {
- m_Rsa = new RSACryptoServiceProvider( 512 );
- m_InternKey = m_Rsa.ExportParameters( true );
- }
В данном листинге мы видим конструктор класса CryptoRsa, который автоматически генерирует ключ длиной 512 бит и экспортирует параметры ключей (true указывает на то, что необходимо экспортировать не только открытый, но и секретный ключ) в переменную m_InternKey.
Далее необходимо сохранить открытый ключ в байтовом формате и отправить серверу. Для этого необходимо немного разобраться в том, из чего состоят ключи RSA. Если кратко – то они состоят из так называемых открытых и секретных экспонент и единого для обоих ключей модуля.
Записываем открытую экспоненту в буфер вывода (C#):
- // Записываем длину экспоненты -> экспоненту -> модуль
- buf.Write( (Byte) m_InternKey.Exponent.Length );
- buf.Write( m_InternKey.Exponent );
- buf.Write( m_InternKey.Modulus );
В данном случае длина экспоненты нужна нам для того, чтобы знать, где именно заканчивается экспонента и начинается модуль (при считывании данных на сервере). После записи отправляем данные серверу.
После того, как сервер принял пакет с ключом, необходимо забрать ключ из пакета и сохранить его. Смотрим (Java):
- // Длина экспоненты
- int expLength = packet.readByte();
- // Получаем байты экспоненты
- byte[] exponent = new byte[ expLength ];
- System.arraycopy(packet.Bytes, packet.Offset, exponent, 0, expLength);
- // Получаем байты модуля
- byte[] modulus = new byte[ 1 packet.Bytes.length – (packet.Offset expLength) ];
- System.arraycopy(packet.Bytes, packet.Offset expLength, modulus, 1, modulus.length – 1 );
- // Магия вуду
- modulus[ 0 ] = 0 ;
- // Сохраняем ключ
- RSAPublicKeySpec rsaPubKeySpec = new RSAPublicKeySpec( new BigInteger(modulus), new BigInteger(exponent) );
- m_ExternPublicKey = (RSAPublicKey)KeyFactory.getInstance(“RSA”).generatePublic(rsaPubKeySpec);
Думаю, здесь не нужно особо еще комментировать код, разве что странную строку, названную мною «магией вуду» :), где мы выставляем первый байт модуля равным нулю. А дело вот в чем – по неизвестным мне причинам реализация RSA в Java требует, чтобы модуль ключа всегда начинался с нуля.
Возможно, это связано с тем, чтобы иметь модуль > 0, т.к. когда я пытался сам реализовать RSA на Java с использованием больших чисел (BigInteger), при неравенстве первого байта нулю получалось отрицательное число. Данный вопрос оставляю Вам, господа Хабравчане, буду очень рад, если кто-нибудь объяснит эту особенность.
Далее идет генерация ключа сервером. Рассмотрим следующий кусок кода (Java):
- // Получаем и инициализируем генератора ключей
- KeyPairGenerator keyGen = KeyPairGenerator.getInstance(“RSA”);
- keyGen.initialize( Config.CRYPTO_KEY_NUM_BITS );
- // Генерируем связку
- m_KeyPair = keyGen.genKeyPair();
- // Получаем открытый и секретный ключи
- m_InternPublicKey = (RSAPublicKey)KeyFactory.getInstance(“RSA”).generatePublic(
- new X509EncodedKeySpec(m_KeyPair.getPublic().getEncoded()));
- m_InternPrivateKey = (RSAPrivateKey)KeyFactory.getInstance(“RSA”).generatePrivate(
- new PKCS8EncodedKeySpec(m_KeyPair.getPrivate().getEncoded()));
Думаю, тут все понятно. Хотя, конечно, если углубляться, то обязательно надо погуглить на тему таких существ, как X509 и PKCS8 (X509EncodedKeySpec и PKCS8EncodedKeySpec).
Следующим этапом является отправка ключей серверу. Производится это практически так же, как и в случае клиента (Java):
- // Записываем длину экспоненты -> экспоненту -> модуль
- bao.write( exponent.length & 0xff ); // записываем в виде байта
- bao.write( exponent );
- bao.write( modulus );
И наконец, получаем ключ на стороне клиента, считываем и сохраняем его (C#):
Защищённость
Цифровая подпись обеспечивает:
- Удостоверение источника документа. В зависимости от деталей определения документа могут быть подписаны такие поля, как «автор», «внесённые изменения», «метка времени» и т. д.
- Защиту от изменений документа. При любом случайном или преднамеренном изменении документа (или подписи) изменится хэш, следовательно, подпись станет недействительной.
- Невозможность отказа от авторства. Так как создать корректную подпись можно лишь, зная закрытый ключ, а он известен только владельцу, то владелец не может отказаться от своей подписи под документом.
Возможны следующие угрозы цифровой подписи:
- Злоумышленник может попытаться подделать подпись для выбранного им документа.
- Злоумышленник может попытаться подобрать документ к данной подписи, чтобы подпись к нему подходила.
- Злоумышленник может попытаться подделать подпись для какого-нибудь документа.
При использовании надёжной хэш-функции, вычислительно сложно создать поддельный документ с таким же хэшем, как у подлинного. Однако, эти угрозы могут реализоваться из-за слабостей конкретных алгоритмов хэширования, подписи, или ошибок в их реализациях.
Тем не менее, возможны ещё такие угрозы системам цифровой подписи:
- Злоумышленник, укравший закрытый ключ, может подписать любой документ от имени владельца ключа.
- Злоумышленник может обманом заставить владельца подписать какой-либо документ, например используя протокол слепой подписи.
- Злоумышленник может подменить открытый ключ владельца (см. управление ключами) на свой собственный, выдавая себя за него.
Концепция алгоритма rsa
Я не буду описывать здесь особенности данного алгоритма, а расскажу именно о том, как его можно использовать в клиент-серверной архитектуре.
Небольшое вступление… Собственно,
(буквенная аббревиатура от фамилий Rivest-Shamir-Adleman) – это криптографический алгоритм с открытым ключом. Это значит, что системой генерируется два разных ключа – открытый и секретный.
Таким образом, мы можем передавать открытый ключ кому угодно, и получать зашифрованные этим ключом сообщения, расшифровать которые можем только мы (с использованием секретного ключа).
Данная концепция представлена на рисунке №1, изображенном выше.
Как Вы видите, ключ после генерации синим персонажем передается зеленому персонажу по незащищенному каналу в открытом виде. Его может перехватить кто угодно, но с его помощью можно только зашифровать сообщение.
Поэтому зеленый персонаж легко получает открытый ключ и производит шифрование своего сообщения с помощью данного ключа.
После этого, он передает зашифрованное сообщение синему персонажу, который производит расшифровку с помощью закрытого ключа.
В пределах двух человек схема довольно-таки простая. Однако, если необходимо организовать такую систему на архитектуре клиент-сервер, возникает ряд дополнительных вопросов, которые мы рассмотрим ниже.
Криптопровайдеры, инициализация и деинициализация
Любой сеанс работы с CryptoAPI начинается с инициализации (получения контекста). Инициализация выполняется при помощи функции CryptAcquireContext. В качестве параметров эта функция принимает имя контейнера ключей, имя криптопровайдера, тип провайдера и флаги, определяющие тип и действия с контейнером ключей и режим работы криптопровайдера:
Криптопровайдер – это сущность (обычно библиотека), реализующая определенный набор криптографических алгоритмов и обеспечивающая работу с ними. Существует около семи стандартных провайдеров, предустановленных в системе. Нам для примеров понадобятся два из них – Microsoft Base Cryptographic Provider (MS_DEF_PROV) и Microsoft Enhanced Cryptographic Provider (MS_ENHANCED_PROV).
| ПРИМЕЧАНИЕ Заметим, что Enhanced-провайдер присутствует только на тех машинах, где установлена поддержка 128-битного шифрования (она автоматически устанавливается вместе с Internet Explorer 6.0). |
Каждый криптопровайдер относится к определенному типу. Это позволяет, перебрав все установленные на машине провайдеры, выбрать те, которые поддерживают нужные алгоритмы. Два упомянутых провайдера имеют тип PROV_RSA_FULL.
Криптопровайдер поддерживает защищенные области, называемые контейнерами ключей. Контейнеры позволяют приложениям сохранять и использовать в дальнейшем сгенерированные один раз ключи, обеспечивая защиту самого ключа от злоумышленника.
| ПРИМЕЧАНИЕ Стандартные криптопровайдеры хранят ключи на диске, в зашифрованном виде. Однако существует потенциальная возможность, что злоумышленник, укравший компьютер или жесткий диск, сможет расшифровать сохраненные ключи. |
Контейнеры бывают двух типов – пользовательские (этот тип используется по умолчанию) и машинные (CRYPT_MACHINE_KEYSET). Пользовательский контейнер доступен только приложениям, выполняемым от имени владельца контейнера. Приложение может использовать такой контейнер для сохранения персональных ключей.
Для первоначального создания контейнера нужно вызвать CryptAcquireContext с флагом CRYPT_NEWKEYSET. Для удаления контейнера требуется указать флаг CRYPT_DELETEKEYSET.
Если приложению не требуется доступ к контейнеру ключей (например, приложение вычисляет хеш MD5), то стоит вызывать CryptAcquireContext с флагом CRYPT_VERIFYCONTEXT, передавая NULL вместо имени контейнера.
Следующий пример демонстрирует инициализацию CryptoAPI для последующего вычисления хеша MD5:
Деинициализация CryptoAPI выполняется с помощью функции CryptReleaseContext, единственным значащим параметром которой является полученный ранее хэндл криптографического контекста.
Симметричные шифры des и 3des
Это одни из немногих симметричных шифров, предоставляемых стандартными криптопровайдерами CryptoAPI. Поскольку DES и 3DES – это практически один и тот же алгоритм (3DES – это DES, применяемый 3 раза подряд), то мы ограничимся примером использования алгоритма 3DES.
| ПРИМЕЧАНИЕ Однако заметим, что для использования алгоритма 3DES требуется Enhanced провайдер, а для DES вполне достаточно Base. Впрочем, DES уже не является стойким по современным меркам алгоритмом, поэтому использовать его стоит лишь там, где надежность шифрования не очень критична. |
Алгоритм 3DES использует разные ключи DES для каждой из своих итераций. Поэтому размер его ключа равен тройному размеру ключа DES, т.е. 192 (64*3) бита. Реально размер ключа 3DES – 168 (56*3) бит, т.к. в DES один байт ключа является контрольным для основных семи. Шифрование и дешифрование выполняются с помощью функций:
BOOL WINAPI CryptEncrypt(HCRYPTKEY hKey,HCRYPTHASH hHash,BOOL Final,DWORD dwFlags,BYTE* pbData,DWORD* pdwDataLen,DWORD dwBufLen); BOOL WINAPI CryptDecrypt(HCRYPTKEY hKey,HCRYPTHASH hHash,BOOL Final,DWORD dwFlags,BYTE* pbData,DWORD* pdwDataLen); |
Параметр hHash позволяет параллельно с шифрованием/дешифрованием проводить хеширование данных для последующей электронной подписи или ее проверки. Флаг Final определяет, является ли шифруемый блок данных последним. Он необходим, поскольку данные можно шифровать по кускам, но для последнего блока всегда выполняется определенная деинициализация алгоритма (освобождаются внутренние структуры), и многие алгоритмы производят добавление (и проверку корректности при дешифровании) заполнителя (padding) после основных данных.
Параметры pbData и pdwDataLen задают адрес буфера и размер шифруемых данных. Для не последнего блока данных (Final=FALSE) размер данных должен быть всегда кратен размеру шифруемого алгоритмом блока (для 3DES и DES этот размер равен 64 битам). Для последнего блока допускается нарушение этого условия.
| ПРИМЕЧАНИЕ Заметим, что зашифрованные данные помещаются в тот же самый буфер поверх исходных. |
Последний параметр функции CryptEncrypt – dwBufLen может показаться странным. Зачем нам размер буфера, если мы и так знаем размер входных данных? Однако на самом деле он необходим. Как я уже упомянул, многие алгоритмы добавляют заполнитель в последний блок после основных данных.
В этом случае размер зашифрованных данных может оказаться больше, чем размер исходных данных. И результат может попросту не вместиться в буфер! Поэтому стоит заранее указать размер буфера, превышающий максимальный размер помещаемых в него открытых данных. Для DES и 3DES максимально возможный довесок составляет 64 бита, т.е. 8 байт (это я установил опытным путем).
В качестве примера шифрования приведу выдержку из демонстрационного проекта encfile:
BYTE buf[BUFFER_SIZE 8]; //8 - запас на padding while(fSize) { if(!::ReadFile(hInFile,buf,BUFFER_SIZE,&dwLen,NULL)) break; dwSzLow=dwLen; if(!::CryptEncrypt(hKey,hHash,fSize<=BUFFER_SIZE,0,buf,&dwSzLow,sizeof(buf))) break; if(!::WriteFile(hOutFile,buf,dwSzLow,&dwSzLow,NULL)) break; fSize-=dwLen; } |
Симметричные шифры des, 3des, rijndael
Симметричные блочные шифры представлены в .NET классами DESCryptoServiceProvider, TripleDESCryptoServiceProvider, RijndaelManaged. Все эти классы являются потомками абстрактного класса SymmetricAlgorithm, описывающего все семейство блочных алгоритмов с симметричными ключами.
Класс описывает свойства, позволяющие манипулировать основными параметрами алгоритма: размером блока, режимом работы, инициализационным вектором, ключом и другими. И методы CreateEncryptor и CreateDecryptor, возвращающие контексты (интерфейс ICryptoTransform) для криптографических трансформаций данных.
Также имеются методы GenerateKey и GenerateIV для генерации ключей и инициализационных векторов. Конкретные реализации наследуются от этого класса (возможно, через другие абстрактные классы – например, DESCryptoServiceProvider наследуется от класса DES, унаследованного от SymmetricAlgorithm).
private SymmetricAlgorithm alg; alg=(SymmetricAlgorithm)RijndaelManaged.Create(); PasswordDeriveBytes pdb=new PasswordDeriveBytes(Password.Text,null); pdb.HashName="SHA512"; //будем использовать SHA512 int keylen=(int)KeySize.SelectedItem; alg.KeySize=keylen; alg.Key=pdb.GetBytes(keylen>>3); alg.Mode=CipherMode.CBC; alg.IV=new Byte[alg.BlockSize>>3]; ICryptoTransform tr=alg.CreateEncryptor(); FileStream instream=new FileStream(inFile.Text,FileMode.Open,FileAccess.Read,FileShare.Read); FileStream outstream=new FileStream(outFile.Text,FileMode.Create,FileAccess.Write,FileShare.None); int buflen=((2<<16)/alg.BlockSize)*alg.BlockSize; byte []inbuf=new byte[buflen]; byte []outbuf=new byte[buflen]; int len; while((len=instream.Read(inbuf,0,buflen))==buflen) { int enclen=tr.TransformBlock(inbuf,0,buflen,outbuf,0); outstream.Write(outbuf,0,enclen); } instream.Close(); outbuf=tr.TransformFinalBlock(inbuf,0,len); outstream.Write(outbuf,0,outbuf.Length); outstream.Close(); alg.Clear(); |
Как можно видеть, ничего сложного в процессе шифрования/дешифрования нет. Использование базового класса SymmetricAlgorithm позволяет свести всю привязку к конкретному алгоритму к одной строчке – созданию экземпляра класса нужного алгоритма.
Стоит, однако, обратить внимание на необходимость явного задания инициализационного вектора (IV), поскольку, в отличие от CryptoAPI, он не инициализируется нулем по умолчанию, а выбирается случайно. На вторые возможные грабли я наступил в коде дешифрования. Размер расшифрованных данных для не финального блока может быть меньше размера шифротекста. Ни с чем подобным в CryptoAPI я не сталкивался. |
Наряду с самостоятельным чтением файла и шифрованием его по блокам, возможен еще вариант с использованием стрима CryptoStream. При этом вы создаете CryptoStream, передавая ему на входе стрим для записи и интерфейс трансформации, а затем просто пишете в этот стрим свои данные. Этот вариант описан в документации по .NET Framework, поэтому я не буду подробно на нем останавливаться.
Создание и проверка эцп документа | блог о шифровании
Постановка задачи
Разработать программу, позволяющую создать ЭЦП, а также программу, осуществляющую проверку правильности ЭЦП.
Основные теоретические сведения
ВЫБОР ПАРАМЕТРОВ СИСТЕМЫ ЭЦП
Параметры системы ЭЦП – числа p,q,a. Эти числа не являются секретными. Конкретный набор их значений может быть общим для группы пользователей.
1.Выбрать простое число p.
2. Выбрать число q так, чтобы q являлось простым делителем числа p-1.
3 .Выработать число a следующим образом:
а) произвольно выбрать число d: 1<d<p-1
б) вычислить f=dp-1/q mod p
в) если f=1, то перейти к а). Если f<>1, то a:=f.
4.Выбрать секретный ключ x.
5. Вычислить открытый ключ пользователя y=ax mod p.
АЛГОРИТМ ВЫРАБОТКИ ПОДПИСИ
1.Вычислить h(M) – значение хеш-функции от каждой строки сообщения М как контрольная сумма 1 в строке сообщения. Если h(M) mod q = 0, присвоить h(M) = 1.
2.Выбрать целое число 0<k<q – секретный ключ
3. Вычислить два значения: r=ak mod p и r1=r mod q. Если r1=0 перейти к п.3.2 и выработать другое значение числа k.
4.С использованием секретного ключа x пользователя вычислить значение s=(x*r1 k*h(M)) mod q. Если s=0 перейти к п.2, в противном случае – конец.
5.Подписью сообщения является вектор <r1>II<s>.
АЛГОРИТМ ПРОВЕРКИ ПОДПИСИ
1.Проверить условие 0<s<q , 0<r1<q. Если хотя бы одно из условий не выполнено, подпись считается недействительной.
2.Вычислить h(M1) – значение хеш-функции от каждой строки полученного сообщения М1 как контрольную сумму 1 в строке сообщения. Если h(M) mod q = 0, присвоить h(M) = 1.
3 Вычислить значение V=(h(M1)) q-2 modq
4Вычислить значения Z1=SV mod q
Z2=(q-r1)Vmod q
5.Вычислить значение U=(az1yz2(mod p))(mod q)
6.Проверить условие r1=u
При совпадении значений u и r1 получатель принимает решение о том, что полученное сообщение подписано данным отправителем и в процессе передачи не нарушена целостность сообщения, т.е. М=М1 . В противном подпись считается недействительной.
Выполнение работы
Проверим правильность работы программы на следующих примерах:

Если изменить значение ЭЦП, то при проверке корректности ЭЦП будет сформировано сообщение об ошибке ЭЦП.
Текст – программы
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs,
StdCtrls;
type
TFlexByte = array of byte;
TForm1 = class(TForm)
Label1: TLabel;
Edit1: TEdit;
Label2: TLabel;
Edit2: TEdit;
Label3: TLabel;
Edit3: TEdit;
Label4: TLabel;
Edit4: TEdit;
Button1: TButton;
Button2: TButton;
OpenDialog1: TOpenDialog;
procedure Button1Click(Sender: TObject);
procedure Button2Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
const
p:word = 31;
q:word = 5;
var
Form1: TForm1;
a:word;
secretKey:word;
openKey:word;
implementation
{$R *.DFM}
function CheckSum(a:TFlexByte):word;
var
i,j:integer;
tmp:byte;
begin
result:=0;
for i:=Low(a) to High(a) do
begin
tmp:=a[i];
for j:=0 to 7 do
begin
if (tmp and 1)<>0 then
result:=result 1;
tmp:=tmp shr 1;
end;
end;
end;
function PowerMod(a:word;b:word;c:word):word;
var
tmp,i:word;
begin
if b=1 then
begin
result:=a mod c;
Exit;
end;
tmp:=(a*a) mod c;
for i:=3 to b do
begin
tmp:=(a*tmp) mod c;
end;
result:=tmp;
end;
function PowerWord(w:word;p:word):word;
var
i:integer;
begin
result:=1;
for i:=1 to p do
result:=result*w;
end;
function Signature(const msg:TFlexByte;var r1:byte;var s:byte;var x:word;var y:word):word;
label
M1,M2;
var
d,f,k,r:word;
begin
// Generate a
Randomize;
M1:
d:=0;
while (d=0)or(d=(p-1)) do
d:=Random(p-1);
f:=PowerMod(d,(p-1)div q, p);
if f=1 then
goto M1
else
a:=f;
// Secret key X | Open key Y
x:=0;
while (x=0)or(x=q) do
x:=Random(q);
y:=PowerMod(a, x, p);
// Calc hash
result:=CheckSum(msg);
if (result mod q)=0 then
result:=1;
// Calc r | r1
M2:
k:=0;
while (k=0)or(k=q) do
k:=Random(q);
r:=PowerMod(a,k,p);
r1:=r mod q;
if r1=0 then
goto M2;
// Calc s
s:=(x*r1 k*result) mod q;
if s=0 then
goto M2;
y:=(y shl 8) a;
end;
function CheckSignature(msg:TFlexByte;r1:byte;s:byte;y:word;var chs:word):boolean;
var
v,z1,z2,u: word;
begin
result:=false;
if (s>0)and(s<q)and(r1>0)and(r1<q) then
begin
chs:=CheckSum(msg);
if (chs mod q)=0 then
chs:=1;
a:=openKey and 255;
y:=openKey shr 8;
v:=PowerMod(chs,q-2,q);
z1:=(s*v)mod q;
z2:=((q-r1)*v) mod q;
u:=(PowerWord(a,z1)*PowerWord(y,z2)mod p)mod q;
result:=(r1=u);
end;
end;
procedure TForm1.Button1Click(Sender: TObject);
var
f:file of byte;
fb:TFlexByte;
signL,signH:byte;
i:integer;
begin
if OpenDialog1.Execute then
begin
AssignFile(f,OpenDialog1.FileName);
Reset(f);
SetLength(fb,FileSize(f));
for i:=Low(fb) to High(fb) do
Read(f,fb[i]);
Edit2.Text:=IntToStr(Signature(fb,signL,signH,secretKey,openKey));
Edit1.Text:=IntToStr(signL) ’ ‘ IntToStr(signH);
Edit3.Text:=IntToStr(secretKey);
Edit4.Text:=IntToStr(openKey);
Write(f,signL);
Write(f,signH);
CloseFile(f);
end;
end;
procedure TForm1.Button2Click(Sender: TObject);
var
f:file of byte;
fb:TFlexByte;
signL,signH:byte;
i:integer;
chs:word;
res:boolean;
begin
if OpenDialog1.Execute then
begin
AssignFile(f,OpenDialog1.FileName);
Reset(f);
SetLength(fb,FileSize(f)-2);
for i:=Low(fb) to High(fb) do
Read(f,fb[i]);
Read(f,signL);
Read(f,signH);
CloseFile(f);
Edit1.Text:=IntToStr(signL) ’ ‘ IntToStr(signH);
openKey:=StrToInt(Edit4.Text);
res:=CheckSignature(fb,signL,signH,openKey,chs);
Edit2.Text:=IntToStr(chs);
if res then
ShowMessage(‘проверка завершена успешно ‘)
else
ShowMessage(‘проверка завершена неуспешно’);
end;
end;
end
.
Вы можете следить за любыми ответами на эту запись через RSS 2.0 ленту.
Вы можете оставить ответ, или trackback с вашего собственного сайта.
Структура и возможности
Блокчейн
— это один из видов распределенного хранения данных, использует 3 ранее известных технологии: одноранговые сети, шифрование и базы данных. База данных представляет из себя цепочку блоков, которая специальным образом шифруется и хранится на всех узлах сети в одном и том же виде (репликация — точная копия).
Блокчейн позволяет безопасно распространять и/или обрабатывать данные между несколькими лицами через недоверенную сеть. Данными может быть что угодно, но наиболее интересным вариантом данных является возможность передачи информации, которая требует наличия третьей доверенной стороны.
Наиболее интересные проекты, где используется блокчейн:
- Monegraph позволяет авторам закрепить права на свою работу и установить правила (и выплаты) за использования их работы;
- La Zooz это децентрализованный Uber. Предлагай свою машину, найди перевозчика без платы Uber’у;
- Augur – это онлайн букмекер. Делай ставки и получай выигрыш;
- Storj.io – это P2P хранилище данных. Сдавай свое неиспользуемое место на диске или найди самое дешевое онлайн хранилище;
- Muse – это распределенная, открытая и прозрачная база данных специально для музыкальной индустрии;
- Ripple позволяет проводить недорогие трансграничные платежи в банки;
- Golem – мировой децентрализованный суперкомпьютер с открытым кодом, доступ к которому может получить любой человек, для выполнения распределенных вычислений (от обработки изображений до проведения исследований и запуска веб-сайтов). Используя Golem, пользователи могут покупать или продавать вычислительные мощности между собой;
- Множество других криптовалют отличающихся высокой анонимностью работы, низкой стоимостью переводов, умными контрактами и т.д.
Фрагменты кода
public class Signature
private X509Certificate2 certificate;
private DateTime date;
private byte[] signedHash;
public X509Certificate2 Certificate
get { return certificate; }
set { certificate = value; }
public DateTime Date
get { return date; }
set { date = value; }
public void Sign(string input, X509Certificate2 cert)
this.certificate = new X509Certificate2( cert);
date = DateTime.Now;
string stringToEncrypt = input date.Ticks;
signedHash = ((RSACryptoServiceProvider)cert.PrivateKey).SignData(Utils.StringToBytes(stringToEncrypt),new MD5CryptoServiceProvider());
public bool IsValid(string input)
string stringToEncrypt = input date.Ticks;
return ((RSACryptoServiceProvider)certificate.PublicKey.Key).VerifyData(Utils.StringToBytes(stringToEncrypt),new MD5CryptoServiceProvider(), signedHash);
public byte[] SignedHash
get { return signedHash; }
set { signedHash = value; }
void DisplaySignatureList()
FileSignatures fileSignatures = ReadSignatures(GetSignaturesFileName(fileNameTextBox.Text));
signatureListTextBox.Text = “”;
foreach (Signature signaure in fileSignatures.Signaures)
string row = “”;
row = signaure.Certificate.Subject;
row =” ” signaure.Date.ToString();
string hash = GetFileHash(fileNameTextBox.Text);
bool valid = signaure.IsValid(hash);
if (valid)
row = “v ” row;
else
row = “x ” row;
signatureListTextBox.Text = row “rn”;
Хеши md5 и sha
Хеш создается вызовом функции CryptCreateHash, принимающей на входе контекст криптопровайдера, идентификатор алгоритма (CALG_MD5 или CALG_SHA) и хендл ключа (для хешей с ключем типа MAC и HMAC). После этого хеш можно вычислять как явно, используя функцию CryptHashData, так и неявно, передавая хэндл хеша в функцию CryptEncrypt.
Вычисление хеша (также как и шифрование) можно производить по частям (например, читая данные в буфер и хешируя содержимое буфера в цикле). После окончания хеширования можно либо подписать хеш (см. ниже), либо получить его значение вызовом:
Размер хеша MD5 равен 128 бит или 16 байтов. Для SHA это 160 бит или 20 байтов. После получения значения хеш использовать уже нельзя. Его нужно разрушить вызовом CryptDestroyHash. Проверка хеша производится точно также, как и его создание – нужно вычислить хеш и сверить полученное значение с сохраненным:
HCRYPTHASH hHash; ::CryptCreateHash(hProv,CALG_MD5,0,0,&hHash); ::CryptHashData(hHash,(BYTE *)&data,dwLen,0); BYTE newHash[16]; dwLen=16; ::CryptGetHashParam(hHash,HP_HASHVAL,newHash,&dwLen,0); if(!memcmp(newHash,oldHash,16)) { } else { } ::CryptDestroyHash(hHash); |
Электронная цифровая подпись
Чтобы информацию внутри транзакций нельзя было подделать, каждая транзакция внутри блока подписывается электронной цифровой подписью (ЭЦП).
Электронно-цифровая подпись – это последовательность байтов, формируемая путем преобразования подписываемой информации по криптографическому алгоритму и предназначенная для проверки авторства электронного документа.
ЭЦП основывается на использовании асимметричного шифрования и хэш-функциях.
Кратко о методах шифрования:
В асимметричных алгоритмах шифрования, шифрование производится с помощью открытого ключа, а расшифровка с помощью закрытого.
Но в асимметричных схемах цифровой подписи подписание производится с применением закрытого ключа, а проверка подписи — с применением открытого, то есть шифруем закрытым, а проверяем открытым (“проверить” это не “расшифровать”, не путайте).
Одним из таких алгоритмов может быть RSA. Выбор ассиметричного шифрования обосновывается тем, что другие участники сети должны убедиться в том, что именно владелец блока внес изменения и подписал блок своей подписью (проверка описана во








