Схема Эль-Гамаля в криптографии

Содержание

Второй учебный алгоритм хеширования
Первый учебный алгоритм хеширования
Схема эль-гамаля в криптографии

Второй учебный алгоритм хеширования

В этом алгоритме

Начальное значение принимается равным числу десятичных разрядов в .
Для каждого десятичного знака числа вычисляется значение
Значение 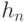, вычисленное для последнего символа, увеличенное на 1, является хеш-значением сообщения: .

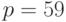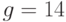Вычисленное по этому алгоритму хеш-значение зависит от всех символов сообщения Пример 9.3Известны значения общих параметров системы Эль-Гамаля: p=59 , g=14 и открытый ключ абонента 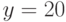y=20 . От абонента получено сообщение 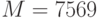M=7569 , снабженное цифровой подписью Эль-Гамаля 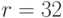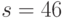r=32 , s=46 . Проверить подлинность цифровой подписи. Хеш-значение сообщение вычисляется с помощью второго учебного алгоритма.

Вычисляем значения 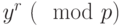$y^{r} ~(mod p)$ и $r^{s} ~(mod p)$ , а затем их произведение по модулю :
В рассматриваемом примере получаем:
Для полученного сообщения вычисляем хеш-значение 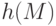по второму учебному алгоритму.
Вычисляем значение $g^{h} ~(mod p)$ .
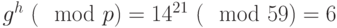В примере $g^{h} ~(mod p)=14^{21}~(mod 59) = 6$ .
Проверяем выполнение равенства 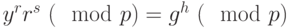$y^{r}r^{s} ~(mod p)=g^h ~(mod p)$ , если равенство выполняется – подпись подлинная, в противном случае – фальшивая.
В нашем примере 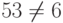. Равенство не выполняется, значит, подпись фальшивая.

Первый учебный алгоритм хеширования

Входом для данного алгоритма является строка, состоящая из букв русского языка.

Выбирается число – вектор инициализации. Число равно длине сообщения в символах.
Для каждого символа сообщения вычисляется значение $h_i=(n_i h_{i-1})^2 ~(mod p)$, $i=1,dots,n$ , где 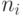– номер -й буквы сообщения в алфавите. Для удобства вычислений ниже приведен нумерованный алфавит.
Значение 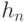, вычисленное для последнего символа, является хеш-значением сообщения: .

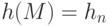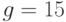
Следует отметить, что вычисленное по этому алгоритму хеш-значение зависит от всех символов сообщения Пример 9.2Выполнить вычисление и проверку подписи сообщения M=text{"БЛЕФ"} по алгоритму Эль-Гамаля. Использовать параметры подписи:

Сформируем хэш-сумму сообщения. Начальное значение равно количеству символов сообщения: . Далее,
Вычисляем число по формуле 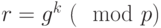. Для рассматриваемого примера получили:
Вычисляем число по формуле , для рассматриваемого примера
Вычисляем значение 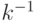$k^{-1}$ по модулю с помощью расширенного алгоритма Евклида. Для рассматриваемого примера значение $k^{-1}=23$ .
Примечание: если полученное значение 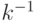$k^{-1}$ – отрицательное, следует взять его по модулю .
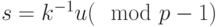Вычисляем число по формуле $s=k^{-1}u (mod p-1)$ . В примере
Цифровая подпись сообщения для рассматриваемого примера: .

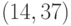Для проверки правильности вычисления полученной цифровой подписи следует произвести ее проверку с помощью открытого ключа абонента и убедиться, что подпись подлинная.

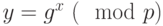Сформируем открытый ключ абонента по формуле $y=g^{x} ~(mod p)$ :
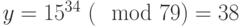Для рассматриваемого примера $y=15^{34} ~(mod 79) = 38$ .
Аналогичным образом вычисляем значения 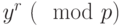$y^{r} ~(mod p)$ и $r^{s} ~(mod p)$ , а затем их произведение по модулю .
В примере получаем:
Вычисляем значение $g^{h} ~(mod p)$ , значение было получено ранее.
В примере $g^{h} ~(mod p)=15^{13} ~(mod 79)= 78$ .
Проверяем выполнение равенства 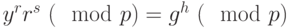$y^{r}r^{s} ~(mod p)=g^h ~(mod p)$ , если равенство выполняется – подпись подлинная, то есть она была вычислена правильно.
В примере получили , равенство выполняется, значит, подпись сгенерирована правильно.

6. Информационные риски: методы оценки и анализа // itportal.ru. [Электронный ресурс]. Режим доступа: http://itportal.ru/science/economy/informatsionnye-riski-metody-otsenk/ (дата обращения: 21.02.2020).

СХЕМА ЭЛЬ-ГАМАЛЯ В КРИПТОГРАФИИ Бадасян Т.С.1, Авагян С.К.2 Email: [email protected]

‘Бадасян Тигран Смбатович — магистрант, факультет прикладной математики и физики; 2Авагян Сурен Константинович — магистрант, кафедра электронных измерительных приборов и метрологии, Национальный политехнический университет Армении, г. Ереван, Республика Армения

Аннотация: в современном мире, в связи с развитием информационных технологий, люди всё чаше используют электронный документооборот. Теперь документы намного удобней передавать, потому что это можно сделать, находясь на расстоянии нескольких тысяч километров друг от друга или вообще проживая в разных странах. В ‘984 была представлена схема Эль-Гамаля. Асимметричный алгоритм, предложенный египетским криптографом Тахером Эль-Гамалем, может использоваться в качестве решения главных задач: шифрования данных и формирования ЭЦП. В статье пойдет речь о схеме Эль-Гамаля в криптографии. Ключевые слова: цифровая подпись, усиленная квалифицированная подпись, логарифмирование, криптографический алгоритм.

ELGAMAL SYSTEM IN CRYPTOGRAPHY Badasyan T.S.1, Avagyan S.K.2

‘Badasyan Tigran Smbatovich – Undergraduate, FACULTY OF APPLIED MATHEMATICS AND PHYSICS; 2Avagyan Suren Konstantinovich – Undergraduate, DEPARTMENT OF ELECTRONIC MEASURING INSTRUMENTS AND METROLOGY, NATIONAL POLYTECHNIC UNIVERSITY OF ARMENIA, YEREVAN, REPUBLIC OF ARMENIA

Abstract: in the modern world with the extreme development of information technologies, people often transfer documents electronically. It is much more convenient to do now, being at a great distance of thousands of kilometers from the recipient, or even in different countries. The ElGamal system was introduced in ‘984. It is an asymmetric algorithm, that was suggested by Egyptian cryptographist Taher Elgamal. The system can be used as a solution of the most important problems of the new millennium: data encryption and digital signature creation. In this article, we will thoroughly discuss the ElGamal system and its impact in cryptography.

Keywords: digital signature, reinforced qualified electronic signature, logarithm, cryptographic algorithm.

УДК 003.26 004.056.5 DOI ‘0.244”/23’2-8089-2020-‘0605

Схема Эль-Гамаля в криптографии: Криптография – наука о методах обеспечения конфиденциальности, целостности данных, аутентификации, а также невозможности отказа от авторства. Основной задачей криптографии является создание наиболее надежного алгоритма шифрования данных. Зачатки криптографии как науки появились ещё четыре тысячи лет назад, когда появилось примитивное шифрование посланий, писем и прочего. С начала двадцатого века в шифровании начинают участвовать вычислительные машины, а с середины семидесятых произошел переход к криптографии с открытым ключом.

Схема Эль-Гамаля. Криптосистема с открытым ключом, основанная на трудности вычисления дискретных логарифмов в конечном поле. Включает в себя алгоритм шифрования и алгоритм цифровой подписи.

Схема была предложена Тахером Эль-Гамалем в 1985 году. Он усовершенствовал систему Диффи-Хеллмана и получил два алгоритма, которые использовались для

шифрования и для обеспечения аутентификации. В отличие от RSA алгоритм Эль-Гамаля не был запатентован и, поэтому, стал более дешевой альтернативой RSA, так как нс требовалась оплата взносов за лицензию.

Вероятностный характер шифрования является преимуществом для схемы Эль-Гамаля, т.к. у схем вероятностного шифрования наблюдается большая стойкость по сравнению со схемами с определенным процессом шифрования [6].

Плюсы данного вида шифрования в том, что этот алгоритм можно использовать свободно, в отличие от RSA. Так же он имеет множество модификаций, т. к. в нём можно использовать различные группы, для которых задача дискретного логарифмирования является трудноразрешимой.

Электронная цифровая подпись (ЭЦП) – это реквизит, который подтверждает подлинность документа, получаемый с помощью криптографического преобразования с применением закрытого ключа, и используемый как юридическим, так и физическим лицом.

В общем, это аналог собственноручной подписи в электронно-цифровом документе для придания ему юридической силы.

Впервые о необходимости ЭЦП заговорили в 1970 году, но её реализация была затруднительна, так как требовался криптостойкий алгоритм. Лишь спустя 7 лет Рональд Ривест, Ади Шамир и Леонард Адлеман разработали криптографический алгоритм RSA, надежность алгоритма основывается на трудности факторизации больших чисел. К 1984 была представлена схема Эль-Гамаля [4].

История электронной цифровой подписи в России начинается с 1994 года, когда был принят первый стандарт – ГОСТ Р34.10 – 94 «Информационная технология. Криптографическая защита информации. Процедуры выработки и проверки электронной цифровой подписи на базе асимметричного криптографического алгоритма».

Создание электронной цифровой подписи на основе схемы Эль-Гамаля происходит следующим образом:

1. У нас имеется сообщение K . Для него мы генерируем хэш-функцию h(K) .

2. Генерируется случайное число p , н берутся такие числа k и q , чтобы выполнялись условия 1 < k < р-1, НОД (k, р -1) = 1 и 1 < q < р .

, . (h(K ) – xr)k 1

3. Вычисляем числа i = q / p и j =-, где X задаётся 1 < x < р .

P -1

Пара чисел (i, j) являются подписью сообщения K.

Получив письмо, второй пользователь должен удостовериться в подлинности этого документа, для этого выполняются следующие действия:

1. Получатель знает закрытый ключ х и открытую пару ключей (р, q) . Вычисляется

значение t = — и проверяются следующие условия: 0 < i < p и 0 < j < p — 1

Подпись неверна, если какое-либо из условий не выполняется.

2. Переходим к вычислению хэш-функции h(K) .

i ^ qh(K)

3. Производится сравнение t — i =-. Если тождество верно – подпись подлинна.

Представленный алгоритм лёг в основу стандартов ЭЦП России и США [1].

Ранее в России использование ЭЦП при заключении сделок регламентировалось Федеральным законом от 10.01.2002 № 1-ФЗ «Об электронной цифровой подписи». Но он долгое время не подвергался обновлениям, которые были так необходимы. Поэтому его отменили и приняли новый Федеральный закон от 06.04.2021 № 63-ФЗ, регулирующий использование ЭП. Согласно закону, разделение электронной подписи на три вида (простая, усиленная неквалифицированная и усиленная квалифицированная) разграничило сферы их применения и, в первую очередь, подтолкнуло к широкому использованию госуслуг в электронном виде [2].

Простые подписи создаются с помощью кодов, паролей и других инструментов, которые позволяют идентифицировать автора документа, но не позволяют проверить его на предмет наличия изменений с момента подписания.

Усиленная неквалифицированная подпись создана с использованием криптографических средств и позволяет определить не только автора документа, но и проверить его на наличие изменений. Для создания таких подписей может использоваться сертификат неаккредитованного центра, можно также вообще обойтись без сертификата, если технические средства позволяют выполнить требования закона.

Усиленная квалифицированная подпись имеет сертификат от аккредитованного центра и создана с помощью подтвержденных ФСБ средств.

Сферы применения электронной цифровой подписи представлены в Таблице 1 [3].

Таблица 1.Сферы применения ЭЦП

Простая Усиленная неквалифици рованная Усиленная квалифицированная

Внутренний и внешний документооборот V V V

Арбитражный суд V V V

Документооборот с физическими лицами V V V

Госуслуги V x V

Контролирующие органы x x V

Электронные торги x x

Выдачу электронной цифровой подписи производят Удостоверяющие центры. Статистика выдачи сертификатов ЭЦП в России представлена на рисунке 1.

Рис. 1. Статистика выдачи сертификатов ЭЦП в России

Сейчас на территории нашей страны они существуют в 85 городах. Любой желающий может получить электронную подпись, например, физическое лицо может предоставить небольшой набор документов (паспорт, СНИЛС, ИНН), оплатить и получить ее в течение 2 часов. Выполняется ЭП в виде смарт-карт и USB-брелоков eToken. Согласно законодательству, срок действия ЭЦП равен 1 году со дня регистрации. После истечения данного срока клиент должен пройти процедуру получения заново [7].

В последние годы электронная цифровая подпись набирает популярность из-за ряда преимуществ: она гарантирует достоверность документации; уменьшает стоимость доставки, хранения и учёта документов; сводит к минимуму риски финансовых потерь за счет увеличения уровня секретности обмена информацией; сокращает время, которое затрачивается на обмен документацией. Всё это заставляет задуматься, ведь каждый желает, чтобы его информация сохраняла свойства целостности и конфиденциальности.

Следует отметить, если задачу дискретного логарифмирования можно решить, значит можно вычислить секретный ключ х зная открытый ключ gx, и пользоваться подписью исходного отправителя. В 1993 году Дэниэл М. Гордон представил алгоритм, способный решать дискретные логарифмы для маленьких чисел в конечном поле GF(p), используя метод решета числового поля [1].

Если развитие компьютерных технологий будет продолжаться в таком же быстром темпе, то уже через несколько лет RSA-алгоритм, который является самым популярным на сегодняшний день, станет неэффективным, а так как его почти невозможно модифицировать, то его использование прекратится. А алгоритм на основе рюкзака станет гораздо популярнее из-за его np-полноты и вариативности модификаций. А ещё он является бесплатным, а с развитием носителей информации, проблема увеличения объёма данных при передаче станет гораздо менее значительной.

Список литературы / References

1. Оценка стойкости криптосистемы Эль-Гамаля // Технические науки в России и за рубежом: материалы IV междунар науч. конф. (г. Москва, январь 2021 г.). М.: Буки-Веди, 2021. С. 14-16.

2. Anjaneyulu G.S.G.N., Sanyasirao A. Distributed Group Key Management Protocol over Non-commutative Division Semirings // Indian Journal of Science and Technology, 2021. Yol. 7 (6). Рp. 871-876.

3. Погудина А.А. Симметричная криптосистема над полукольцом с делением. // Информационные технологии и прикладная математика. Межвузовский сборник аспирантских и студенческих работ, 2021. Вып. 5. С. 130-133.

4. Корепанова Н.Л., Лебедева М.А. Системно-теоретический подход к проектированию симметричных крптогра-фических систем // Системы контроля. Севастополь: ИПТС, 2021. Вып. 5 (25). С. 59-64.

5. Поляков А.С. Анализ возможностей алгоритмов международного стандарта «Облегченная криптография». ISO/ШС 29192-2:2021 / А.С. Поляков, В.Е. Самсонов // Информатика, 2021. № 3. С. 107-112.

6. On the relationship between functional encryption, obfuscation, and fully homomorphic encryption / J. Alwen [et al.] // Cryptography and Coding – 14th IMA Intern. Conf.. IMACC-2021. Oxford. UK, 2021. P. 65-84.

7. Русецкая И.А. История криптографии в Западной Европе в раннее Новое время. СПб.: Центр гуманитарных инициатив. Университетская книга. СПб., 2021.