НОУ ИНТУИТ | Лекция | Хэш-функции и электронная подпись

Содержание

Что такое электронная подпись — простым языком для новичков мира цифровой экономики
В каком виде хранить ЭЦП?
1 Хэш-функции
2.1 Общие положения
2.2 Схема Эль-Гамаля
Второй учебный алгоритм хеширования
Где применяется электронная подпись
Зачем нужна электронная подпись?
Как выбрать сертификат электронной подписи?
Области применения электронной подписи
Первый учебный алгоритм хеширования
Тенденции рынка электронной подписи
Усиленная электронная подпись
Этап третий

Что такое электронная подпись — простым языком для новичков мира цифровой экономики

30 октября 2021

Что такое электронная подпись — простым языком для новичков мира цифровой экономики

В статье даны ответы на вопросы: «Как выглядит электронная подпись», «Как работает ЭЦП», рассмотрены ее возможности и основные компоненты, а также представлена наглядная пошаговая инструкция процесса подписания файла электронной подписью.

Что такое электронная подпись?

Электронная подпись – это не предмет, который можно взять в руки, а реквизит документа, позволяющий подтвердить принадлежность ЭЦП ее владельцу, а также зафиксировать состояние информации/данных (наличие, либо отсутствие изменений) в электронном документе с момента его подписания.

Справочно:

Сокращенное название (согласно федеральному закону № 63) — ЭП, но чаще используют устаревшую аббревиатуру ЭЦП (электронная цифровая подпись). Это, например, облегчает взаимодействие с поисковиками в интернете, так как ЭП может также означать электрическую плиту, электровоз пассажирский и т.д.

Согласно законодательству РФ, квалифицированная электронная подпись — это эквивалент подписи, проставляемой «от руки», обладающий полной юридической силой. Помимо квалифицированной в России представлены еще два вида ЭЦП:

— неквалифицированная — обеспечивает юридическую значимость документа, но только после заключения дополнительных соглашений между подписантами о правилах применения и признания ЭЦП, позволяет подтвердить авторство документа и проконтролировать его неизменность после подписания,

— простая — не придает подписанному документу юридическую значимость до заключения дополнительных соглашений между подписантами о правилах применения и признания ЭЦП и без соблюдении законодательно закрепленных условий по ее использованию (простая электронная подпись должна содержаться в самом документе, ее ключ применяться в соответствии с требованиями информационной системы, где она используется, и прочее согласно ФЗ-63, ст.9), не гарантирует его неизменность с момента подписания, позволяет подтвердить авторство. Ее применение не допускается в случаях, связанных с государственной тайной.

Возможности электронной подписи

Физическим лицам ЭЦП обеспечивает удаленное взаимодействие с государственными, учебными, медицинскими и прочими информационными системами через интернет.

Юридическим лицам электронная подпись дает допуск к участию в электронных торгах, позволяет организовать юридически-значимый электронный документооборот (ЭДО) и сдачу электронной отчетности в контролирующие органы власти.

Возможности, которые предоставляет ЭЦП пользователям, сделали ее важной составляющей повседневной жизни и рядовых граждан, и представителей компаний.

Что означает фраза «клиенту выдана электронная подпись»? Как выглядит ЭЦП?

Сама по себе подпись является не предметом, а результатом криптографических преобразований подписываемого документа, и ее нельзя «физически» выдать на каком-либо носителе (токене, smart-карте и т.д.). Также ее нельзя увидеть, в прямом значении этого слова; она не похожа на росчерк пера либо фигурный оттиск. О том, как «выглядит» электронная подпись, расскажем чуть ниже.

Справочно:

Криптографическое преобразование — это зашифровка, которая построена на использующем секретный ключ алгоритме. Процесс восстановления исходных данных после криптографического преобразования без данного ключа, по мнению специалистов, должен занять большее время, чем срок актуальности извлекаемой информации.

Flash-носитель — это компактный носитель данных, в состав которого входит flash-память и адаптер (usb-флешка).

Токен — это устройство, корпус которого аналогичен корпусу usb-флешки, но карта памяти защищена паролем. На токене записана информация для создания ЭЦП. Для работы с ним необходимо подключение к usb-разъему компьютера и введения пароля.

Smart-карта — это пластиковая карта, позволяющая проводить криптографические операции за счет встроенной в нее микросхемы.

Sim-карта с чипом — это карта мобильного оператора, снабженная специальным чипом, на которую на этапе производства безопасным образом устанавливается java-приложение, расширяющее ее функциональность.

Как же следует понимать фразу «выдана электронная подпись», которая прочно закрепилась в разговорной речи участников рынка? Из чего состоит электронная подпись?

Выданная электронная подпись состоит из 3 элементов:

1 – средство электронной подписи, то есть необходимое для реализации набора криптографических алгоритмов и функций техническое средство. Это может быть либо устанавливаемый на компьютер криптопровайдер (КриптоПро CSP, ViPNet CSP), либо самостоятельный токен со встроенным криптопровайдером (Рутокен ЭЦП, JaCarta ГОСТ), либо «электронное облако». Подробнее прочитать о технологиях ЭЦП, связанных с использованием «электронного облака», можно будет в следующей статье Единого портала Электронной подписи.

Справочно:

Криптопровайдер — это независимый модуль, выступающий «посредником» между операционной системой, которая с помощью определенного набора функций управляет им, и программой или аппаратным комплексом, выполняющим криптографические преобразования.

Важно: токен и средство квалифицированной ЭЦП на нем должны быть сертифицированы ФСБ РФ в соответствии с требованиями федерального закона № 63.

2 – ключевая пара, которая представляет из себя два обезличенных набора байт, сформированных средством электронной подписи. Первый из них – ключ электронной подписи, который называют «закрытым». Он используется для формирования самой подписи и должен храниться в секрете. Размещение «закрытого» ключа на компьютере и flash-носителе крайне небезопасно, на токене — отчасти небезопасно, на токене/smart-карте/sim-карте в неизвлекаемом виде — наиболее безопасно. Второй — ключ проверки электронной подписи, который называют «открытым». Он не содержится в тайне, однозначно привязан к «закрытому» ключу и необходим, чтобы любой желающий мог проверить корректность электронной подписи.

3 – сертификат ключа проверки ЭЦП, который выпускает удостоверяющий центр (УЦ). Его назначение — связать обезличенный набор байт «открытого» ключа с личностью владельца электронной подписи (человеком или организацией). На практике это выглядит следующим образом: например, Иван Иванович Иванов (физическое лицо) приходит в удостоверяющий центр, предъявляет паспорт, а УЦ выдает ему сертификат, подтверждающий, что заявленный «открытый» ключ принадлежит именно Ивану Ивановичу Иванову. Это необходимо для предотвращения мошеннической схемы, во время развертывания которой злоумышленник в процессе передачи «открытого» кода может перехватить его и подменить своим. Таким образом, преступник получит возможность выдавать себя за подписанта. В дальнейшем, перехватывая сообщения и внося изменения, он сможет подтверждать их своей ЭЦП. Именно поэтому роль сертификата ключа проверки электронной подписи крайне важна, и за его корректность несет финансовую и административную ответственность удостоверяющий центр.

В соответствии с законодательством РФ различают:

— «сертификат ключа проверки электронной подписи» формируется для неквалифицированной ЭЦП и может быть выдан удостоверяющим центром;

— «квалифицированный сертификат ключа проверки электронной подписи» формируется для квалифицированной ЭЦП и может быть выдан только аккредитованным Министерством связи и массовых коммуникаций УЦ.

Условно можно обозначить, что ключи проверки электронной подписи (наборы байт) — понятия технические, а сертификат «открытого» ключа и удостоверяющий центр — понятия организационные. Ведь УЦ представляет собой структурную единицу, которая отвечает за сопоставление «открытых» ключей и их владельцев в рамках их финансово-хозяйственной деятельности.

Подводя итог вышеизложенному, фраза «клиенту выдана электронная подпись» состоит из трех слагаемых:

Клиент приобрел средство электронной подписи.
Он получил «открытый» и «закрытый» ключ, с помощью которых формируется и проверяется ЭЦП.
УЦ выдал клиенту сертификат, подтверждающий, что «открытый» ключ из ключевой пары принадлежит именно этому человеку.

Вопрос безопасности

Требуемые свойства подписываемых документов:

целостность;
достоверность;
аутентичность (подлинность; «неотрекаемость» от авторства информации).

Их обеспечивают криптографические алгоритмы и протоколы, а также основанные на них программные и программно-аппаратные решения для формирования электронной подписи.

С определенной долей упрощения можно говорить, что безопасность электронной подписи и сервисов, предоставляемых на ее основе, базируется на том, что «закрытые» ключи электронной подписи хранятся в секрете, в защищенном виде, и что каждый пользователь ответственно хранит их и не допускает инцидентов.

Примечание: при приобретении токена важно поменять заводской пароль, таким образом, никто не сможет получить доступ к механизму ЭЦП кроме ее владельца.

Как подписать файл электронной подписью?

Для подписания файла ЭЦП нужно выполнить несколько шагов. В качестве примера рассмотрим, как поставить квалифицированную электронную подпись на свидетельство на товарный знак Единого портала Электронной подписи в формате .pdf. Нужно:

1. Кликнуть на документ правой кнопкой мышки и выбрать криптопровайдер (в данном случае КриптоАРМ) и графу «Подписать».

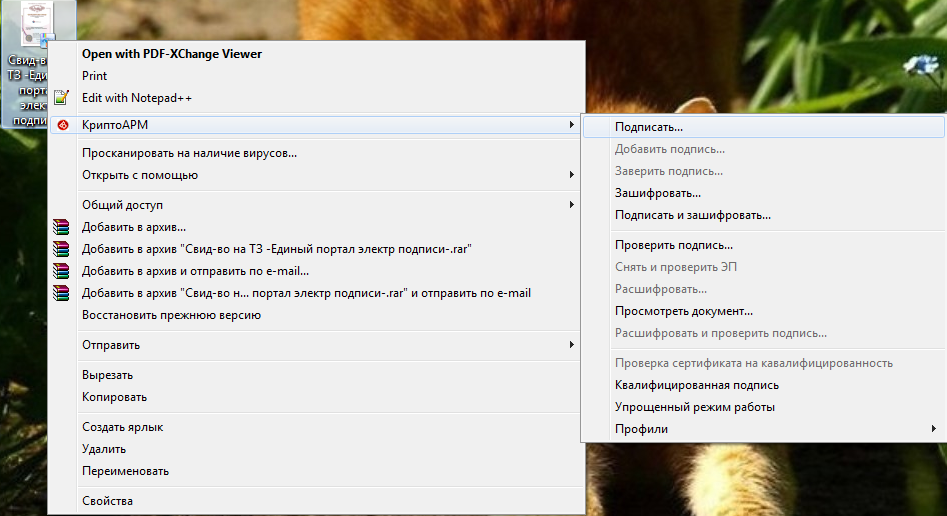
Подписание файла электронной подписью

2. Пройти путь в диалоговых окнах криптопровайдера:

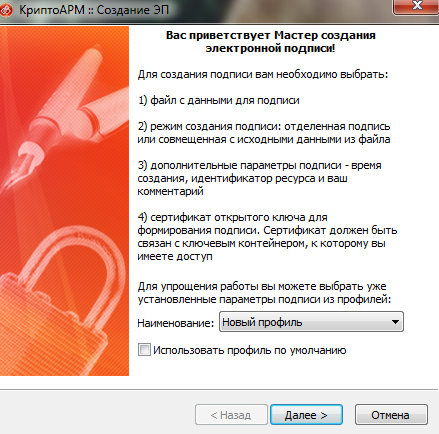
Запуск мастера создания электронной подписи

Выбрать кнопку «Далее».

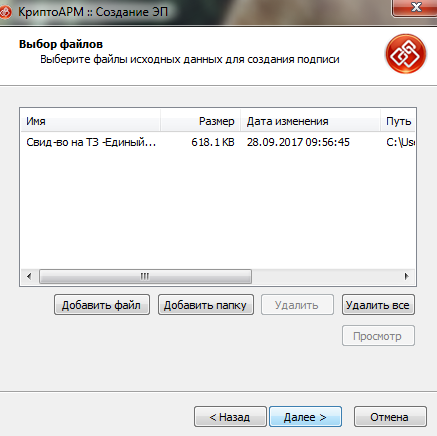
Выбор файлов исходных данных для создания электронной подписи

На этом шаге при необходимости можно выбрать другой файл для подписания, либо пропустить этот этап и сразу перейти к следующему диалоговому окну.

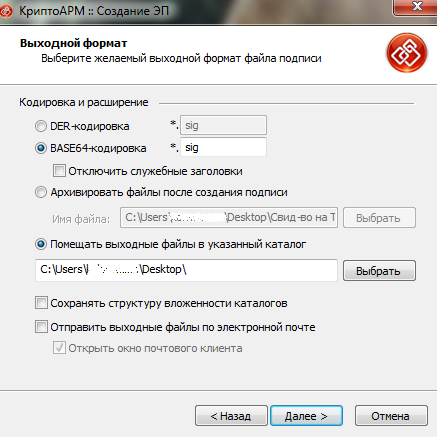
Выбор желаемого выходного формата электронной подписи

Поля «Кодировка и расширение» не требуют редактирования. Ниже можно выбрать, где будет сохранен подписанный файл. В примере, документ с ЭЦП будет размещен на рабочем столе (Desktop).

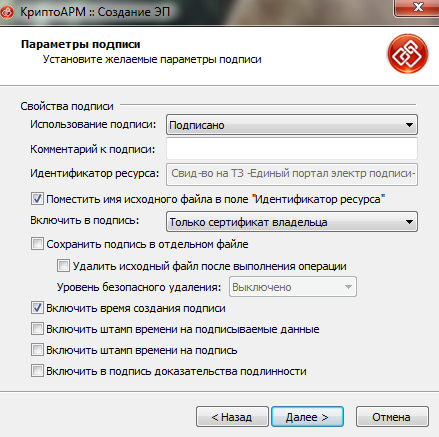
Установка желаемых параметров электронной подписи

В блоке «Свойства подписи» выбираете «Подписано», при необходимости можно добавить комментарий. Остальные поля можно исключить/выбрать по желанию.

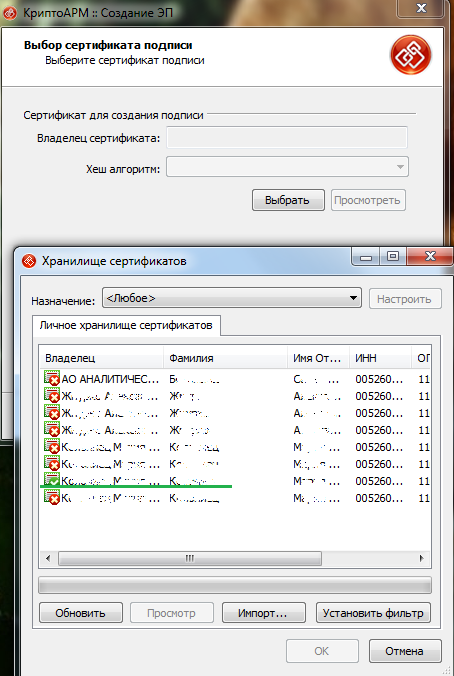
Выбор сертификата электронной подписи

Из хранилища сертификатов выбираете нужный.

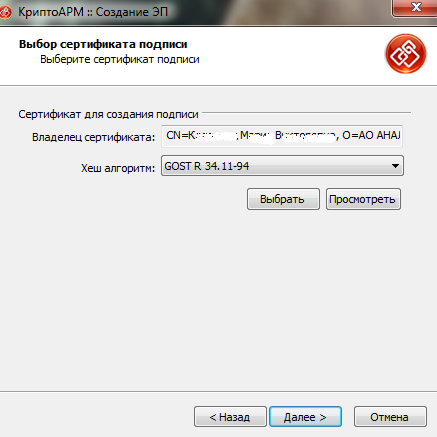
Проверка правильности Владельца сертификата электронной подписи

После проверки правильности поля «Владелец сертификата», нажимайте кнопку «Далее».

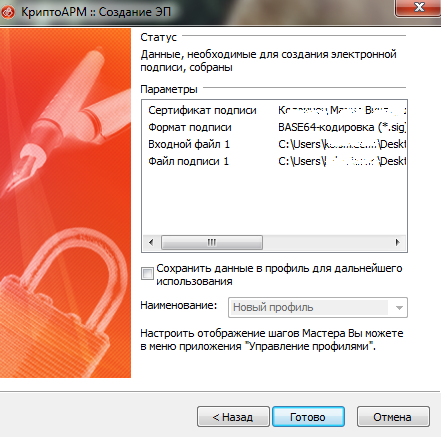
Финальная проверка данных для создания электронной подписи

В данном диалоговом окне проводится финальная проверка данных, необходимых для создания электронной подписи, а затем после клика на кнопку «Готово» должно всплыть следующее сообщение:

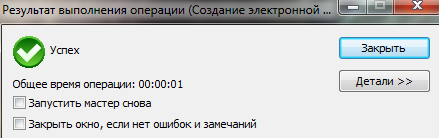
Подтверждение создания электронной подписи

Успешное окончание операции означает, что файл был криптографически преобразован и содержит реквизит, фиксирующий неизменность документа после его подписания и обеспечивающий его юридическую значимость.

Итак, как же выглядит электронная подпись на документе?

Для примера берем файл, подписанный электронной подписью (сохраняется в формате .sig), и открываем его через криптопровайдер.

Файл, подписанный электронной подписью, на рабочем столе

Фрагмент рабочего стола. Слева: файл, подписанный ЭП, справа: криптопровайдер (например, КриптоАРМ).

Визуализация электронной подписи в самом документе при его открытии не предусмотрена ввиду того, что она является реквизитом. Но есть исключения, например, электронная подпись ФНС при получении выписки из ЕГРЮЛ/ЕГРИП через онлайн сервис условно отображается на самом документе. Скриншот можно найти по ссылке.

Но как же в итоге «выглядит» ЭЦП, вернее, как факт подписания обозначается в документе?

Открыв через криптопровайдер окно «Управление подписанными данными», можно увидеть информацию о файле и подписи.

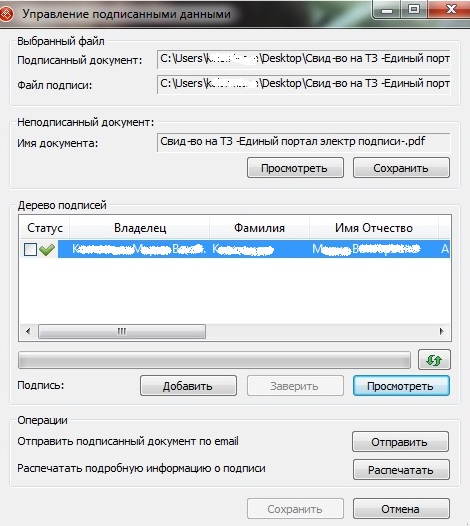
Управление подписанными электронной подписью данными

При нажатии на кнопку «Посмотреть» появляется окно, содержащее информацию о подписи и сертификате.

Информация об электронной подписи и сертификате

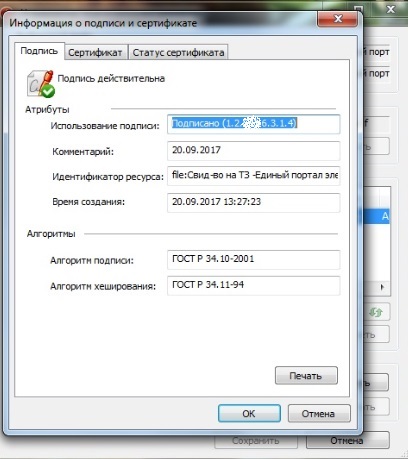
Последний скриншот наглядно демонстрирует как выглядит ЭЦП на документе «изнутри».

Приобрести электронную подпись можно по ссылке.

Задавайте другие вопросы по теме статьи в комментариях, эксперты Единого портала Электронной подписи обязательно ответят Вам.

Статья подготовлена редакцией Единого портала Электронной подписи ecpexpert.ru с использованием материалов компании SafeTech.

При полном или частичном использовании материала гиперссылка на www.ecpexpert.ru обязательна.

В каком виде хранить ЭЦП?

Электронная цифровая подпись представляет собой набор символов в текстовом формате, поэтому поместить ее можно на любом носителе. Однако для правильного функционирования, необходимо соответствующее программное обеспечение. Поэтому логично хранить файл в следующих местах:

Локальные хранилища операционной системы
Это наиболее простой и самый экономичный способ хранения электронной подписи. Такие хранилища предусмотрены в каждой ОС. При установленном Windows, подпись будет размещаться в его реестре. Однако у этого способа есть несколько недостатков. Воспользоваться подписью можно только на компьютере, где она храниться. А в случае повреждения или переустановки операционной системы, доступ к электронной подписи будет утерян. Для пользования подписью, размещенной в ОС, необходима установка криптопровайдера. Это программа, преобразовывающая криптографические алгоритмы.
Токены
Это устройство, внешне напоминающее флешку, предназначенное для безопасного хранения ЭЦП. Как и любой другой носитель, токен имеет ограниченный объем памяти, он варьируется от 32Кб до 256Кб. Обычно один сертификат требует от 4 до 10Кб, поэтому Вы можете самостоятельно рассчитать, сколько подписей вместиться в данный носитель. Для полноценной работы с подписью в этом случае тоже требуется наличие криптопровайдера. В 2021 году в наличии есть токены со встроенным программным обеспечением, они имеют маркировку ЭЦП или ГОСТ.
Хранилища облачного типа
В этом варианте ЭЦП размещается на удаленном сервисе. При этом доступ к ней осуществляется посредством специального интерфейса API, либо через привязку к номеру мобильного телефона (подписать можно путем отправки СМС). Это значительно оптимизирует работу с электронной подписью, не требует специализированного программного обеспечения, да и наличия компьютера вообще. Управлять всеми действиями можно напрямую через мобильный телефон. Из минусов данного способа – не все государственные организации принимают на рассмотрение документы, подписанные облачной ЭЦП.

1 Хэш-функции

Определение 9.1Хэш-функции – это функции, предназначенные для “сжатия” произвольного сообщения, записанного, как правило, в двоичном алфавите, в некоторую битовую последовательность фиксированной длины, называемую сверткой.

Хэш-функции применяются для тестирования логических устройств, для быстрого поиска и проверки целостности записей в базах данных.

В криптографии хэш-функции применяются для решения следующих задач:

При решении первой задачи для каждого набора данных вычисляется значение хеш-функции (называемое кодом аутентификации сообщения или имитовставкой), которое передается или хранится вместе с самими данными.

При получении данных пользователь вычисляет значение свертки и сравнивает его с имеющимся контрольным значением. Несовпадение говорит о том, что данные были изменены. При решении второй задачи, аутентификации источника данных, мы имеем дело с не доверяющими друг другу сторонами.

В связи с этим подход, при котором обе стороны обладают одним и тем же секретным ключом, уже не применим. В такой ситуации применяют схемы цифровой подписи, позволяющие осуществить аутентификацию источника данных. Как правило, при этом сообщение, прежде чем быть подписано личной подписью, основанной на секретном ключе пользователя, “сжимается” с помощью хеш-функции, выполняющей функцию кода обнаружения ошибок.

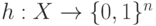Определение 9.2Обозначим через множество, элементы которого будем называть сообщениями, – натуральное число. Хеш-функцией называется всякая легко вычислимая функция $h: X rightarrow {0,1}^n$ .

Кроме того, хэш-функцию можно понимать, как отображение из множества сообщений в некоторое ограниченное подмножество целых неотрицательных чисел.

Обычно число возможных сообщений значительно превосходит число возможных значений сверток, в силу чего для каждого значения свертки имеется большое множество прообразов, то есть сообщений с заданным значением хеш-функции. Заметим, что при случайном и равновероятном выборе сообщений условие равномерности распределения значений хеш-функции эквивалентно наличию одинакового числа прообразов для каждого значения свертки.

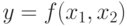
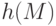
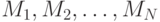
Как правило, хеш-функции строят на основе так называемых одношаговых сжимающихся функцийдлина свертки. Для получения значения длина сообщения не кратна вектор. Если функциявектор можно положить равным нулевому вектору. Если же функциявектор можно составить из фрагментов указывающих на дату, время, номер сообщения и т.п.При таком подходе свойства хеш-функции

2.1 Общие положения

Появление криптографии с открытым ключом позволило решать задачи, которые ранее считались неразрешимыми. К таким задачам относится использование цифрового аналога собственноручной подписи абонента – электронной цифровой подписи (ЭЦП).

Цифровая подпись (ЭЦП) для сообщения является числом, зависящим от самого сообщения и от секретного ключа, известного только подписывающему. Важное требование: подпись должна допускать проверку без знания секретного ключа. При возникновении спорной ситуации, связанной с отказом от факта подписи либо с возможной подделкой подписи, третья сторона должна иметь возможность разрешить спор.

Задачи, которые решает подпись:

Для реализации схемы ЭЦП необходимы два алгоритма: алгоритм генерации подписи и алгоритм проверки. Надежность схемы ЭЦП определяется сложностью следующих задач:

Заметим, что между ЭЦП и собственноручной подписью имеются различия, хотя они и служат для решения одинаковых задач. Так, ЭЦП зависит от подписываемого текста, различна для разных тестов. Кроме того, ЭЦП требует дополнительных механизмов, реализующих алгоритмы ее вычисления и проверки.

Наконец, принципиальной сложностью, возникающей при использовании ЭЦП, является необходимость создания инфраструктуры открытых ключей. Эта инфраструктура состоит из центров сертификации открытых ключей и обеспечивает возможность своевременного подтверждения достоверности открытой информации, необходимой для проверки ЭЦП, что необходимо для предотвращения подделки подписи.

2.2 Схема Эль-Гамаля

См. [1]

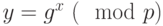
Безопасность схемы основана на трудности вычисления дискретных логарифмов в конечном поле. Для генерации пары ключей выбирается простое число $y=g^{x} ~(mod p)$

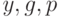
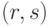
Для проверки подписи нужно убедиться, что

Первое замечание о выборе

Схема Эль-Гамаля послужила образцом для построения большого семейства во многом сходных по своим свойствам схем подписи.

Пример 9.1Выберем 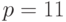p =11 и g = 2 , а секретный ключ x = 8 .

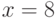Вычислим:

Открытым ключом являются

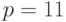
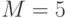
Теперь находим

Итак, подпись представляет собой пару: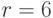

Для проверки подписи убедимся, что:

Второе замечание. При вычислении подписи целесообразно использовать хэш-образ сообщения, а не само сообщение 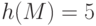хеширования и шифрования с открытым ключом (в частности, RSA или Эль-Гамаля).

Алгоритм формирования подписи выглядит следующим образом:

Пусть – подписываемое сообщение. Отправитель вычисляет хеш-значение подписываемого сообщения 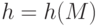. Значение должно удовлетворять неравенству .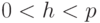
Отправитель выбирает случайное число , , 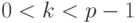взаимно простое с , и вычисляет числа:
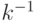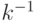$k^{-1}$ – число, обратное по модулю , $k^{-1}$ существует, так как и – взаимно просты.
Подпись 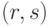добавляется к сообщению, и тройка 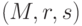передается получателю.

Проверка подписи: получатель заново вычисляет хеш-значение присланного сообщения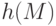

Если подпись верна, то это равенство выполняется.

Отметим, что число

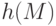
Второй учебный алгоритм хеширования

В этом алгоритме

Начальное значение принимается равным числу десятичных разрядов в .
Для каждого десятичного знака числа вычисляется значение
Значение 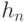, вычисленное для последнего символа, увеличенное на 1, является хеш-значением сообщения: .

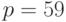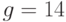Вычисленное по этому алгоритму хеш-значение зависит от всех символов сообщения Пример 9.3Известны значения общих параметров системы Эль-Гамаля: p=59 , g=14 и открытый ключ абонента 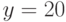y=20 . От абонента получено сообщение 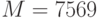M=7569 , снабженное цифровой подписью Эль-Гамаля 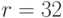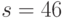r=32 , s=46 . Проверить подлинность цифровой подписи. Хеш-значение сообщение вычисляется с помощью второго учебного алгоритма.

Вычисляем значения 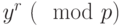$y^{r} ~(mod p)$ и $r^{s} ~(mod p)$ , а затем их произведение по модулю :
В рассматриваемом примере получаем:
Для полученного сообщения вычисляем хеш-значение 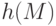по второму учебному алгоритму.
Вычисляем значение $g^{h} ~(mod p)$ .
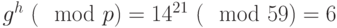В примере $g^{h} ~(mod p)=14^{21}~(mod 59) = 6$ .
Проверяем выполнение равенства 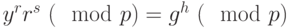$y^{r}r^{s} ~(mod p)=g^h ~(mod p)$ , если равенство выполняется – подпись подлинная, в противном случае – фальшивая.
В нашем примере 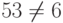. Равенство не выполняется, значит, подпись фальшивая.

Где применяется электронная подпись

В целом области применения электронной подписи можно разделить на пять больших блоков.

1. Отчетность

Отчетность в ФНС явилась толчком для развития электронного документооборота (ЭДО). На сегодняшний день почти все контролирующие органы принимают отчетность в электронном виде. Законодательным катализатором оказалась отчетность по НДС, которая с 2021 года стала обязательной в электронном виде.

Определенные виды отчетности пока можно сдавать и в электронном виде и в бумажном. Но сфера применения электронной подписи постоянно расширяется, так как к процессу ЭДО подключается все больше органов исполнительной власти.

2. Электронные торги

Массово электронная подпись начала применяться в 2021 году, когда процедуры торгов перевели на пять государственных федеральных электронных торговых площадок. Это был старт большой отрасли, которая с тех пор непрерывно развивается.

На текущий момент существует не менее двухсот электронных торговых площадок, которые организуют торги по различным отраслям, но по-прежнему действуют пять крупных федеральных электронных площадок.

Когда был введен в действие закон 223-ФЗ, который регулирует закупки государственных организаций, все эти компании стали обязаны организовывать закупки в соответствии с требованиями 223-ФЗ. Часть таких закупок проходит на электронных торговых площадках, которых порядка 150 и на которых применяются различные сертификаты, по большей части сертифицированные.

Законом установлено требование на использование неквалифицированной электронной подписи, на которую налагаются дополнительные требования. При этом отрасль постепенно идет в сторону унификации, к повсеместному переходу на применение квалифицированной электронной подписи, в том числе в торгах по 44-ФЗ.

Отдельная отрасль электронных торгов — это продажа имущества банкротов. Существует ряд площадок, на которых можно проводить такие торги. Действует отдельное законодательство, которое в том числе устанавливает требование, чтобы использовалась квалифицированная электронная подпись.

Коммерческие торги в секторе B2B

Здесь не действует никаких законодательных рамок. Поэтому площадки все организуют по своему усмотрению: кто-то осуществляет коммерческие торги при помощи квалифицированной электронной подписи, кто-то при помощи неквалифицированной электронной подписи, а некоторые площадки даже при помощи простой электронной подписи.

3. Государственные порталы

Госпорталы — довольно разнородная категория информационных систем, которые не обязательно созданы для отчетности, хотя многие из них очень близки к этой теме.

Зачем нужна электронная подпись?

Назначение ее вполне понятно. В последние годы компании активно переходят с бумажного документооборота на электронный, поэтому обычным для нас подписям и печатям на бумаге нужен аналог. Этим аналогом, по сути, является ЭП.

ЭП решает несколько основных задач. Первая — неотрекаемость. Благодаря ЭП можно доказать, что конкретный человек является автором документа, даже если он отказывается это признавать. Вторая задача — обеспечение подтверждения целостности документа, то есть подтверждение того, что после создания документа и его подписания никто не вносил туда каких-либо изменений (как намеренно, так и случайно).

Допустим, у вас есть платежное поручение в банк на 10 000 руб., подписанное ЭП. Злоумышленник может поменять сумму с 10 000 руб. на 1 млн, чтобы перевести себе в 100 раз больше денег. Для предотвращения таких случаев ЭП фиксирует конечное содержимое электронного документа и позволяет установить, вносились ли в него изменения.

Как выбрать сертификат электронной подписи?

На сегодняшний день существует много видов сертификатов. Законодательство меняется, информационные системы выдвигают различные требования, и вопрос выбора часто встает перед клиентом, так как клиент не может разобраться, какой сертификат ему нужен для той или иной задачи. На что ему следует ориентироваться?

В первую очередь нужно отталкиваться от той информационной системы, в которой планируется применять сертификат. Обычно клиент представляет, для чего ему нужна ЭП. Например, он хочет принять участие в торгах или работать с порталом Росреестра. Требования информационной системы к сертификату, как правило, указываются на сайте информационной системы, в нормативных документах, которые определяют регламент действия этой информационной системы.

На сайте СКБ Контур есть удобный мастер подбора сертификата, который позволяет клиенту ответить на несколько вопросов, касающихся области применения требуемого сертификата, и на выходе получить один или несколько типов сертификатов, полностью закрывающих потребности. Специальный тариф «Электронная подпись 3.0» подходит для решения большинства задач.

Области применения электронной подписи

В зависимости от вида подписи можно говорить о различных областях применения. Простая ЭП используется в интернет-банках физлицами и иногда юрлицами, на различных электронных порталах, например, на Портале госуслуг. Чтобы пользоваться этим порталом, нужно по СНИЛС получить пароль, с помощью которого можно зайти на портал и заказать услугу — допустим, оформление загранпаспорта. Это действие будет юридически значимым.

Можно выделить пять основных областей применения ЭП:

Различные электронные торги — для усиленной ЭП.
Государственные информационные системы. Существует Система межведомственного электронного взаимодействия (СМЭВ), которая объединяет различные государственные органы разного уровня и позволяет им общаться между собой в электронном виде, она взаимодействует в том числе и с Порталом госуслуг. Эта огромная инфраструктура базируется на использовании КЭП. Отдельно существующие информационные системы, например, система Росреестра, также используют КЭП. Спектры услуг, которые оказывают такие информационные системы, обширный: каждая система решает задачи своего ведомства в разном объеме. Где-то это довольно полный перечень услуг — как в Росреестре, где-то — точечные услуги, которые могут быть оказаны через эти порталы. Но везде применяется КЭП.
ЭДО между хозяйствующими субъектами и документооборот внутри компании. Для использования ЭП существует несколько сценариев, все зависит от желания самого бизнеса, от требований к обеспечению юридической значимости используемых электронных документов, поэтому спектр используемой ЭП разнится — от самой незащищенной простой ЭП до КЭП.

Первый учебный алгоритм хеширования

Входом для данного алгоритма является строка, состоящая из букв русского языка.

Выбирается число – вектор инициализации. Число равно длине сообщения в символах.
Для каждого символа сообщения вычисляется значение $h_i=(n_i h_{i-1})^2 ~(mod p)$, $i=1,dots,n$ , где 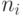– номер -й буквы сообщения в алфавите. Для удобства вычислений ниже приведен нумерованный алфавит.
Значение 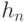, вычисленное для последнего символа, является хеш-значением сообщения: .

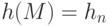Следует отметить, что вычисленное по этому алгоритму хеш-значение зависит от всех символов сообщения Пример 9.2Выполнить вычисление и проверку подписи сообщения M=text{"БЛЕФ"} по алгоритму Эль-Гамаля. Использовать параметры подписи:

Сформируем хэш-сумму сообщения. Начальное значение равно количеству символов сообщения: . Далее,
Вычисляем число по формуле 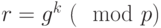. Для рассматриваемого примера получили:
Вычисляем число по формуле , для рассматриваемого примера
Вычисляем значение 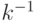$k^{-1}$ по модулю с помощью расширенного алгоритма Евклида. Для рассматриваемого примера значение $k^{-1}=23$ .
Примечание: если полученное значение 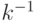$k^{-1}$ – отрицательное, следует взять его по модулю .
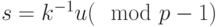Вычисляем число по формуле $s=k^{-1}u (mod p-1)$ . В примере
Цифровая подпись сообщения для рассматриваемого примера: .

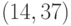Для проверки правильности вычисления полученной цифровой подписи следует произвести ее проверку с помощью открытого ключа абонента и убедиться, что подпись подлинная.

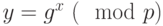Сформируем открытый ключ абонента по формуле $y=g^{x} ~(mod p)$ :
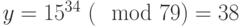Для рассматриваемого примера $y=15^{34} ~(mod 79) = 38$ .
Аналогичным образом вычисляем значения 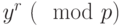$y^{r} ~(mod p)$ и $r^{s} ~(mod p)$ , а затем их произведение по модулю .
В примере получаем:
Вычисляем значение $g^{h} ~(mod p)$ , значение было получено ранее.
В примере $g^{h} ~(mod p)=15^{13} ~(mod 79)= 78$ .
Проверяем выполнение равенства 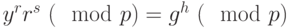$y^{r}r^{s} ~(mod p)=g^h ~(mod p)$ , если равенство выполняется – подпись подлинная, то есть она была вычислена правильно.
В примере получили , равенство выполняется, значит, подпись сгенерирована правильно.

Тенденции рынка электронной подписи

Расширение сфер использования

Сейчас насчитается более 60 отраслей применения электронной подписи. Ежегодно прибавляется порядка двух десятков отраслей применения электронной подписи.

Облачная электронная подпись

Пока нет однозначного мнения от регуляторов по поводу того, как она должна функционировать. На текущий момент существуют различные решения, которые в той или иной степени применяются. Часть из них квалифицируется как облачная квалифицированная подпись, часть — как облачная неквалифицированная подпись.

Есть страны, которые активно применяют эту технологию и позволяют своим гражданам и бизнесу пользоваться электронной подписью на SIM-карте мобильного телефона (Азербайджан, страны Прибалтики). В России эта технология пока только развивается.

Повышение рисков и, как следствие, ужесточение регуляции

По мере увеличения количества областей, где применяется электронная подпись, повышаются и риски, связанные с мошенническими действиями. Злоумышленники пытаются найти различные лазейки, чтобы получить выгоду. Чем больше таких возможностей, тем больше ответственности возлагается на информационные системы и аккредитованные центры.

Сокращение количества удостоверяющих центров

Это один из главных трендов, возникший как следствие повышения рисков. Последняя из мер — применение поправок к закону об электронной подписи, которые увеличили требования к удостоверяющим центрам.

Усиленная электронная подпись

В КЭП и НЭП заложены криптографические алгоритмы. Чем эти виды подписи отличаются друг от друга?

Средствами и алгоритмами, при помощи которых создается ЭП. В случае с НЭП на них не накладываются никакие дополнительные ограничения. Это может быть американский, российский, белорусский и другой криптографический алгоритм.
ПО для работы с ЭП. В случае с НЭП на средства ЭП не накладываются ограничения. В случае с КЭП, наоборот, к средствам предъявляются дополнительные требования — они должны быть сертифицированы в ФСБ и соответствовать определенным стандартам. Это сразу же влечет за собой ограничение на криптографический алгоритм, а именно должны применяться только российские алгоритмы в соответствии с ГОСТ. Накладываются требования и на сам сертификат ЭП по его структуре, то есть существуют жесткие требования, определяющие структуру этого сертификата.
Аккредитованный удостоверяющий центр (УЦ). Квалифицированные сертификаты ЭП должны выпускаться УЦ, которые прошли процедуру аккредитации в Минкомсвязи. Такие УЦ удовлетворяют ряду довольно серьезных требований, гарантирующих их надежность.
Структура сертификата ЭП. Квалифицированный сертификат ЭП должен удовлетворять требованиям по структуре, например, содержать СНИЛС владельца. К неквалифицированным таких требований не предъявляется.

Таким образом, суть отличия между НЭП и КЭП прозрачна: так как на КЭП накладывается несколько жестких ограничений, ее юридический статус выше. КЭП — это единственная подпись, которая признается равной собственноручной подписи без дополнительных мероприятий.

Что касается НЭП, то для признания ее равной собственноручной подписи требуются дополнительные соглашения между участниками электронного документооборота (ЭДО) либо отдельный нормативно-правовой акт, регламентирующий факт равнозначности. Например, если между двумя компаниями осуществляется ЭДО, то документы они подписывают ЭП.

В этом случае компании могут пользоваться НЭП, но тогда им придется заключить между собой соглашение, устанавливающее правила использования и признания этой ЭП. Они могут пользоваться, допустим, американской криптографией, встроенной в Windows, не прикладывая никаких дополнительных усилий.

При этом в суде им нужно будет доказывать юридическую значимость на основе данного соглашения. В случае допущения в соглашении о документообороте каких-то ошибок, значимость электронного документа может быть не признана. Если те же самые компании ведут ЭДО, используя КЭП, то им не понадобятся дополнительные соглашения друг с другом, а юридическая значимость документов будет в силу ФЗ признаваться автоматически.

Этап третий

Заявитель оплачивает счет, собирает необходимый пакет документов и приходит в сервисный центр для получения сертификата.

В сервисном центре он представляет комплект документов, который сотрудник центра визирует и проверяет на корректность. Далее он подписывает договор, осуществляет прочие формальности и в зависимости от того, какой способ ему удобнее, получает уже готовый защищенный носитель (внешне похожий на флешку), на котором хранится секретный ключ и сертификат, или самостоятельно на своем рабочем месте (в случае с квалифицированным сертификатом ЭП) получает сертификат через специальный сайт Личный кабинет УЦ.

Самый важный этап в процессе получения сертификата электронной подписи — это подготовка необходимого комплекта документов. Если комплект собран правильно, то процесс проходит быстро.

Есть ряд дополнительных услуг, которые можно заказать в сервисном центре, например, ускоренное получение сертификата в течение часа после представления документов. Такая услуга может понадобиться при экстренной необходимости участия в торгах.