Однонаправленные хэш-функции на основе симметричных блочных алгоритмов
Однонаправленную хэш-функцию можно
построить, используя симметричный блочный алгоритм. Наиболее очевидный подход
состоит в том, чтобы шифровать сообщение М посредством блочного алгоритма в
режиме СВС или СFВ с помощью фиксированного ключа и некоторого вектора
инициализации IV.
Последний блок шифртекста можно рассматривать в качестве
хэш-значения сообщения М. При таком подходе не всегда возможно построить
безопасную однонаправленную хэш-функцию, но всегда можно получить код
аутентификации сообщения МАС (Message Authentication Code).
Более безопасный вариант хэш-функции
можно получить, используя блок сообщения в качестве ключа, предыдущее
хэш-значение – в качестве входа, а текущее хэш-значение – в качестве выхода.
Реальные хэш-функции проектируются еще более сложными. Длина блока обычно
определяется длиной ключа, а длина хэш-значения совпадает с длиной блока.
Поскольку большинство блочных алгоритмов являются 64-битовыми, некоторые
схемы хэширования проектируют так, чтобы хэш-значение имело длину, равную двойной длине блока.
Если принять, что получаемая
хэш-функция корректна, безопасность схемы хэширования базируется на безопасности
лежащего в ее основе блочного алгоритма. Схема хэширования, у которой длина
хэш-значения равна длине блока, показана на рис.3. Ее работа описывается
выражениями:
Н0 = Iн,
Нi = ЕA(В) Å С,где
Å
– сложение по модулю 2 (исключающее ИЛИ);
Iн
– некоторое случайное начальное значение;
А, В, С
могут принимать значения
Мi,
Нi-1, (МiÅ
Нi-1)
или быть константами.

Рис.3. Обобщенная схема формирования хэш-функции
Сообщение М разбивается на блоки
Мi принятой длины, которые обрабатываются поочередно.
Три различные переменные А, В, С
могут принимать одно из четырех возможных значений, поэтому в принципе можно
получить 64 варианта общей схемы этого типа. Из них 52 варианта являются либо
тривиально слабыми, либо небезопасными. Остальные 12 схем безопасного хэширования,
у которых длина хэш-значения равна длине блока перечислены в табл.1.
| Таблица 1 | ||||||||||||||||||||||||||
|
Первые четыре схемы хэширования,
являющиеся безопасными при всех атаках, приведены на рис.4.
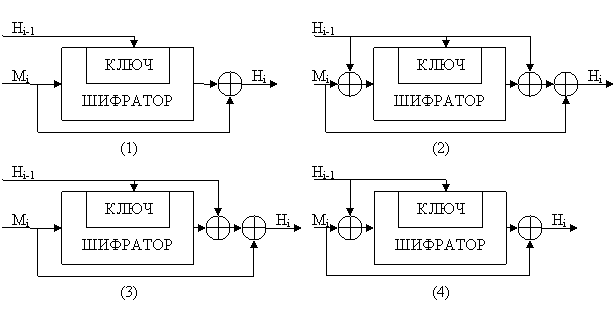
Рис.4. Четыре схемы безопасного хэширования
Недостатком хэш-функций, спроектированных на основе блочных алгоритмов, является несколько
заниженная скорость работы. Дело в том, что ту же самую стойкость относительно двух основных
требований к хэш-функции можно обеспечить за гораздо меньшее количество операций над входными
данными.
Но для этого алгоритм необходимо изначально проектировать специально, исходя из
тандема требований (стойкость, скорость). Далее рассмотрены три самостоятельных алгоритма
криптостойкого хэширования, получивших наибольшее распространение на сегодняшний день.
Алгоритм MD5 (Message Digest №5) разработан Роналдом Риверсом.
MD5 использует 4 многократно повторяющиеся преобразования над тремя 32-битными величинами
U, V и W:
f(U,V,W)=(U AND V) OR ((NOT U) AND W) g(U,V,W)=(U AND W) OR (V AND (NOT W)) h(U,V,W)=U XOR V XOR W k(U,V,W)=V XOR (U OR (NOT W)).
В алгоритме используются следующие константы:
- начальные константы промежуточных величин –
H[0]=6745230116, H[1]=EFCDAB8916, H[2]=98BADCFE16, H[3]=1032547616;
- константы сложения в раундах –
y[j]=HIGHEST_32_BITS(ABS(SIN(j 1))) j=0...63,
где функция HIGHEST_32_BITS(X) отделяет 32 самых старших бита из двоичной записи
дробного числа X, а операнд SIN(j 1) считается взятым в радианах; - массив порядка выбора ячеек в раундах –
z[0...63] = (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 1, 6, 11, 0, 5, 10, 15, 4, 9, 14, 3, 8, 13, 2, 7, 12, 5, 8, 11, 4, 1, 4, 7, 10, 13, 0, 3, 6, 9, 12, 15, 2, 0, 7, 14, 5, 12, 3, 10, 1, 8, 15, 6, 13, 4, 11, 2, 9); - массив величины битовых циклических сдвигов влево –
s[0...63] = (7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22, 5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20, 4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23, 6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21).
На первоначальном этапе входной блок данных дополняется одним битом “1”. Затем к нему
добавляется такое количество битов “0”, чтобы остаток от деления блока на 512 составлял 448.
Наконец, к блоку добавляется 64-битная величина, хранящая первоначальную длину документа.
Получившийся входной поток имеет длину кратную 512 битам.
Каждый 512-битный блок, представленный в виде 16 32-битных значений
X[0]…X[15], проходит через сжимающую функцию, которая перемешивает его
со вспомогательным блоком (H[0],H[1],H[2],H[3]):
(A,B,C,D) = (H[0],H[1],H[2],H[3]) цикл по j от 0 до 15 T = (A f(B,C,D) x[z[j]] y[j]) ROL s[j] (A,B,C,D) = (D,B T,B,C) конец_цикла цикл по j от 16 до 31 T = (A g(B,C,D) x[z[j]] y[j]) ROL s[j] (A,B,C,D) = (D,B T,B,C) конец_цикла цикл по j от 32 до 47 T = (A h(B,C,D) x[z[j]] y[j]) ROL s[j] (A,B,C,D) = (D,B T,B,C) конец_цикла цикл по j от 48 до 63 T = (A k(B,C,D) x[z[j]] y[j]) ROL s[j] (A,B,C,D) = (D,B T,B,C) конец_цикла (H[0],H[1],H[2],H[3]) = (H[0] A,H[1] B,H[2] C,H[3] D)
После того, как все 512-битные блоки прошли через процедуру перемешивания, временные
переменные H[0],H[1],H[2],H[3], а 128-битное значение подается на выход хэш-функции.
Алгоритм MD5, основанный на предыдущей разработке Роналда Риверса MD4, был призван
дать еще больший запас прочности к криптоатакам. MD5 очень похож на MD4. Отличие состоит в
простейших изменениях в алгоритмах наложения и в том, что в MD4 48 проходов основного
преобразования, а в MD5 – 64.
Несмотря на большую популярность, MD4 “медленно, но верно” был
взломан. Сначала появились публикации об атаках на упрощенный алгоритм. Затем было заявлено о
возможности найти два входных блока сжимающей функции MD4, которые порождают одинаковый
выход.
Наконец, в 1995 году было показано, что найти коллизию, т.е. “хэш-двойник” к
произвольному документу, можно менее чем за минуту, а добиться “осмысленности” фальшивого
документа (т.е. наличия в нем только ASCII-символов с определенными “разумными” законами
расположения) – всего лишь за несколько дней.
Алгоритм безопасного хэширования SНА
(Secure Hash Algorithm) разработан НИСТ и АНБ США в рамках стандарта безопасного
хэширования SHS (Secure Hash Standard) в 1992 г. Алгоритм хэширования SНА
предназначен для использования совместно с алгоритмом цифровой подписи DSА.
При вводе сообщения М произвольной
длины менее 264 бит алгоритм SНА вырабатывает 160-битовое выходное
сообщение, называемое дайджестом сообщения МD (Message Digest). Затем этот
дайджест сообщения используется в качестве входа алгоритма DSА, который
вычисляет цифровую подпись сообщения М.
Такой же дайджест сообщения должен
вычисляться пользователем, проверяющим полученную подпись, при этом в качестве
входа в алгоритм SНА используется полученное сообщение М.
Алгоритм хэширования SНА назван
безопасным, потому что он спроектирован таким образом, чтобы было вычислительно
невозможно восстановить сообщение, соответствующее данному дайджесту, а также
найти два различных сообщения, которые дадут одинаковый дайджест.
Рассмотрим подробнее работу алгоритма
хэширования SНА. Прежде всего исходное сообщение М дополняют так, чтобы оно
стало кратным 512 битам. Дополнительная набивка сообщения выполняется следующим
образом: сначала добавляется единица, затем следуют столько нулей, сколько
необходимо для получения сообщения, которое на 64 бита короче, чем кратное 512,
и наконец добавляют 64-битовое представление длины исходного
сообщения.
Инициализируется пять 32-битовых переменных в виде:
А = 0х67452301 В = 0хЕFСDАВ89 С = 0х98ВАDСFЕ D = 0x10325476 Е = 0хС3D2Е1F0
Затем начинается главный цикл
алгоритма. В нем обрабатывается по 512 бит сообщения поочередно для всех
512-битовых блоков, имеющихся в сообщении. Первые пять переменных А, В, С, D, Е
копируются в другие переменные a, b, с, d, е:
а = А, b = В, с = С, d = D, е = Е
Главный цикл содержит четыре цикла по
20 операций каждый. Каждая операция реализует нелинейную функцию от трех из пяти
переменных а, b, с, d, е, а затем производит сдвиг и сложение.
Алгоритм SНА имеет следующий набор
нелинейных функций:
ft (Х, Y, Z) = (X Ù Y) Ú ((Ø X) Ù Z) для t = 0...19, ft (Х, Y, Z) =Х Å Y Å Z для t = 20...39, ft (Х, Y, Z) = (X Ù Y) Ú (X Ù Z) Ú (Y Ù Z) для t = 40...59, ft (Х, Y, Z) = Х Å Y Å Z для t = 60...79,
где
t
– номер операции.
В алгоритме используются также четыре константы:
Кt = 0х5А827999 для t = 0...19, Кt = 0х6ЕD9ЕВА1 для t = 20...39, Кt = 0х8F1ВВСDС для t = 40...59, Кt = 0хСА62С1D6 для t = 60...79.
Блок сообщения преобразуется из шестнадцати 32-битовых слов
(М0…М15) в восемьдесят 32-битовых слов
(W0…W79) с помощью следующего алгоритма:
Wt = Мt для t = 0...15, Wt = (Wt-3Å Wt-8Å Wt-14Å Wt-16) <<< 1 для t = 16...79,
где
t
– номер операции,
Wtt
-й субблок расширенного сообщения,
<<<
S
– циклический сдвиг влево на
S
бит.
С учетом введенных обозначений главный цикл из восьмидесяти операций можно
описать так:
цикл по t от 0 до 79 ТЕМР = (а <<< 5) ft (b, c, d) е Wt Кt е = d d = с с = (b <<< 30) b = а а = ТЕМР конец_цикла
Схема выполнения одной операции показана на рис.5.
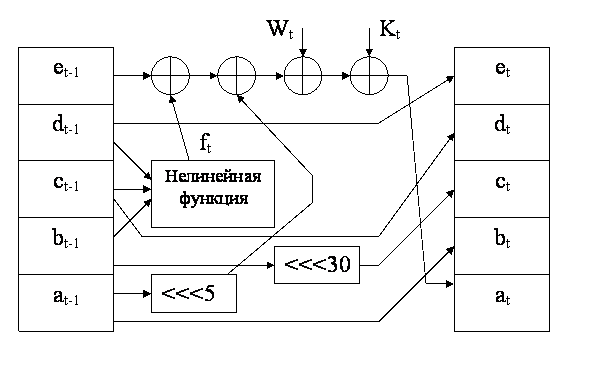
Рис.5. Схема выполнения одной операции алгоритма SHA
После окончания главного цикла
значения а, b, с, d, е складываются с А, В, С, D, Е соответственно, и
алгоритм приступает к обработке следующего 512-битового блока данных. Окончательный выход
формируется в виде конкатенации значений А, В, С, D, Е.
Отличия SHA от MD5 состоят в следующем:
- SНА выдает 160-битовое хэш-значение, поэтому он более устойчив к атакам
полного перебора и атакам “дня рождения”, чем MD5, формирующий 128-битовые хэш-значения. - Сжимающая функция SHA состоит из 80 шагов, а не из 64 как в MD5.
- Расширение входных данных производится не простым их повторение в другом порядке, а
рекуррентной формулой. - Усложнен процесс перемешивания
Проблема аутентификации данных и электронная цифровая подпись
При обмене электронными документами
по сети связи существенно снижаются затраты на обработку и хранение документов,
убыстряется их поиск. Но при этом возникает проблема аутентификации автора
документа и самого документа, т.е. установления подлинности автора и отсутствия
изменений в полученном документе.
Целью аутентификации электронных документов является их защита от возможных
видов злоумышленных действий, к которым относятся:
- активный перехват – нарушитель, подключившийся к сети, перехватывает документы (файлы) и изменяет их;
- маскарад – абонент С посылает документ абоненту В от имени абонента А;
- ренегатство – абонент А заявляет, что не посылал сообщения абоненту В, хотя на самом деле послал;
- подмена – абонент В изменяет или формирует новый документ и заявляет, что получил его от абонента А;
- повтор – абонент С повторяет ранее переданный документ, который абонент А посылал абоненту В.
При обработке документов в
электронной форме совершенно непригодны традиционные способы установления
подлинности по рукописной подписи и оттиску печати на бумажном документе.
Принципиально новым решением является электронная цифровая подпись (ЭЦП).
Электронная цифровая подпись используется для аутентификации
текстов, передаваемых по телекоммуникационным каналам. Функционально она
аналогична обычной рукописной подписи и обладает ее основными достоинствами:
- удостоверяет, что подписанный текст исходит от лица, поставившего подпись;
- не дает самому этому лицу возможности отказаться от обязательств, связанных с подписанным текстом;
- гарантирует целостность подписанного текста.
Цифровая подпись представляет собой
относительно небольшое количество дополнительной цифровой информации,
передаваемой вместе с подписываемым текстом.
Система ЭЦП включает две
процедуры: 1) процедуру постановки подписи; 2) процедуру проверки подписи. В
процедуре постановки подписи используется секретный ключ отправителя сообщения,
в процедуре проверки подписи – открытый ключ отправителя.
При формировании ЭЦП отправитель прежде всего вычисляет хэш-функциюh(М)
подписываемого текста М. Вычисленное значение хэш-функции h(М) представляет
собой один короткий блок информации m, характеризующий весь текст М в целом.
При проверке ЭЦП
получатель сообщения снова вычисляет хэш-функцию m = h(М) принятого по каналу
текста М, после чего при помощи открытого ключа отправителя проверяет,
соответствует ли полученная подпись вычисленному значению m
хэш-функции.
Принципиальным моментом в системе ЭЦП является невозможность
подделки ЭЦП пользователя без знания его секретного ключа подписывания.
В качестве подписываемого документа может быть использован любой файл.
Подписанный файл создается из неподписанного путем добавления в него одной или
более электронных подписей.
Каждая подпись содержит следующую информацию:
- дату подписи;
- срок окончания действия ключа данной подписи;
- информацию о лице, подписавшем
файл (Ф.И.0., должность, краткое наименование фирмы); - идентификатор подписавшего (имя открытого ключа);
- собственно цифровую подпись.
Хэш-функция (англ. hash – мелко измельчать и перемешивать) предназначена для сжатия
подписываемого документа до нескольких десятков или сотен бит. Хэш-функция
h(·) принимает в качестве аргумента сообщение (документ) М произвольной
длины и возвращает хэш-значение h(М)
=Н фиксированной длины. Обычно хэшированная
информация является сжатым двоичным представлением основного сообщения
произвольной длины. Следует отметить, что значение хэш-функции h(М) сложным
образом зависит от документа М и не позволяет восстановить сам документ М.
Хэш-функция должна удовлетворять целому ряду условий:
- хэш-функция должна быть чувствительна к всевозможным изменениям в тексте М,
таким как вставки, выбросы, перестановки и т.п.; - хэш-функция должна обладать свойством необратимости, то есть задача подбора документа М',
который обладал бы требуемым значением хэш-функции, должна быть вычислительно неразрешима; - вероятность того, что значения хэш-функций двух различных документов (вне зависимости от их длин)
совпадут, должна быть ничтожно мала.
Большинство хэш-функций строится на
основе однонаправленной функции f(·), которая образует выходное значение
длиной n при задании двух входных значений длиной n. Этими входами являются
блок исходного текста М, и хэш-значение Нi-1 предыдущего блока текста
(рис.1).

Рис.1. Построение однонаправленной хэш-функции
Нi = f(Мi, Нi-1) .
Хэш-значение, вычисляемое при вводе
последнего блока текста, становится хэш-значением всего сообщения М.
В результате однонаправленная хэш-функция всегда формирует выход
фиксированной длины n (независимо от длины входного текста).
2.4 Цифровая подпись на эллиптических кривых
См. [3]
В качестве международного стандарта принят американский алгоритм цифровой подписи на эллиптических кривых (ECDSA). В этом стандарте используются эллиптические кривые как над полем простого порядка, так и над полем характеристики 2. Однако криптографически стойких кривых над полем характеристики 2 сравнительно мало. Поэтому мы рассмотрим ЭЦП на эллиптических кривых, заданных над полем большей характеристики.
Замечание. В России официально принят стандарт ЭЦП на эллиптических кривых над полем большей характеристики – ГОСТ 34.10-2001 “Информационная технология. Криптографическая защита информации. Процессы формирования и проверки электронной цифровой подписи”. Выбор кривой и точки на ней подразумевает решение ряда вспомогательных задач. Прежде всего, это подсчет количества точек на кривой. Если 






Для получения криптографически стойкой системы ЭЦП должны выполняться следующие условия:
- Порядок точки
 , используемой в системе ЭЦП, должен быть простым числом
, используемой в системе ЭЦП, должен быть простым числом 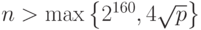 .
. 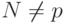 и
и 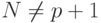 , где
, где  – порядок кривой.
– порядок кривой. для всех
для всех  , где
, где  настолько велико, что вычислить дискретный логарифм в
настолько велико, что вычислить дискретный логарифм в  за приемлемое время невозможно.
за приемлемое время невозможно.
Замечание. В настоящее время значение 







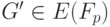
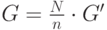


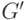

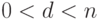
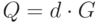

Алгоритм цифровой подписи rsа
Первой и наиболее известной во всем
мире конкретной системой ЭЦП стала система RSА, математическая схема которой
была разработана в 1977 г. в Массачуссетском технологическом институте
США.
Сначала необходимо вычислить пару
ключей (секретный ключ и открытый ключ). Для этого отправитель (автор)
электронных документов вычисляет два больших простых числа Р и Q, затем находит
их произведение
N = Р * Q
и значение функции
j (N) = (Р-1)(Q-1).Далее отправитель вычисляет число Е из условий:
Е £ j (N), НОД (Е, j (N)) = 1
и число D из условий:
D < N, Е*D º 1 (mod j (N)).
Пара чисел (Е, N) является открытым
ключом. Эту пару чисел автор передает партнерам по переписке для проверки его
цифровых подписей. Число D сохраняется автором как секретный ключ для
подписывания.
Обобщенная схема формирования и
проверки цифровой подписи RSА показана на рис.6.
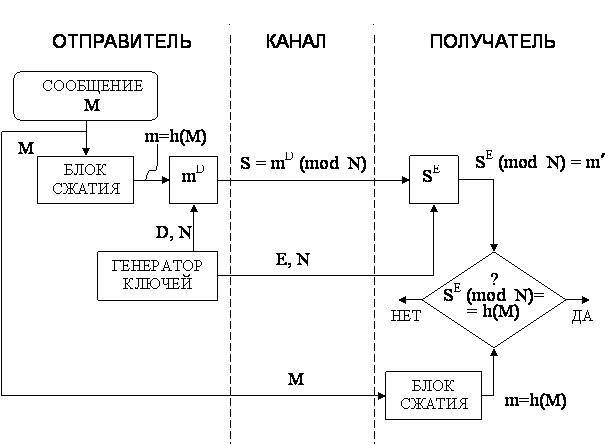
Рис.6. Обобщённая схема цифровой подписи RSA
Допустим, что отправитель хочет
подписать сообщение М перед его отправкой. Сначала сообщение М (блок информации,
файл, таблица) сжимают с помощью хэш-функции h(·) в целое число m:
m = h(М).
Затем вычисляют цифровую подпись S под электронным документом М, используя
хэш-значение m и секретный ключ D:
S = mD (mod N).
Пара (М,S) передается
партнеру-получателю как электронный документ М, подписанный цифровой подписью S,
причем подпись S сформирована обладателем секретного ключа D.
После приема пары (М,S) получатель
вычисляет хэш-значение сообидения М двумя разными способами. Прежде всего он
восстанавливает хэш-значение m’, применяя криптографическое преобразование
подписи S с использованием открытого ключа Е:
m' = SE (mod N).
Кроме того, он находит результат
хэширования принятого сообщения М с помощью такой же хэш-функции
h(·):
m = h(М).
Если соблюдается равенство вычисленных значений, т.е.
SE ( mod N ) = h ( М ),
то получатель признает пару
(М,S)
подлинной. Доказано, что только обладатель секретного ключа
D
может сформировать
цифровую подпись
S
по документу
М
, а определить секретное число
D
по открытому
числу
Е
не легче, чем разложить модуль
N
на множители.
Кроме того, можно строго
математически доказать, что результат проверки цифровой подписи S будет
положительным только в том случае, если при вычислении S был использован
секретный ключ D, соответствующий открытому ключу Е. Поэтому открытый ключ
Е иногда называют “идентификатором” подписавшего.
Недостатки алгоритма цифровой подписи RSА.
- При вычислении модуля N, ключей Е
и D для системы цифровой подписи RSА необходимо проверять большое количество
дополнительных условий, что сделать практически трудно. Невыполнение любого из
этих условий делает возможным фальсификацию цифровой подписи со стороны того,
кто обнаружит такое невыполнение. При подписании важных документов нельзя
допускать такую возможность даже теоретически. - Для обеспечения криптостойкости цифровой подписи RSА по отношению к попыткам
фальсификации на уровне, например, национального стандарта США на шифрование информации
(алгоритм DES), т.е. 1018, необходимо использовать при вычислениях
N, D и Е целые числа не
менее 2512 (или около 10154) каждое, что требует больших
вычислительных затрат, превышающих на 20…30% вычислительные затраты других
алгоритмов цифровой подписи при сохранении того же уровня криптостойкости. - Цифровая подпись RSА уязвима к так
называемой мультипликативной атаке. Иначе говоря, алгоритм цифровой подписи RSА
позволяет злоумышленнику без знания секретного кпюча D сформировать подписи под
теми документами, у которых результат хэширования можно вычислить как
произведение результатов хэширования уже подписанных документов.
Пример. Допустим, что
злоумышленник может сконструировать три сообщения М1,
М2, М3, у которых хэш-значения
m1 = h (М1), m2 = h (М2), m3 = h (М3) ,
причем
m3 = m1 * m2 (mod N) .
Допустим также, что для двух сообщений М1 и М2
получены законные подписи
S1 = m1D (mod N) S2 = m2D (mod N) .
Тогда злоумышленник может легко вычислить подпись S3 для документа
М3, даже не зная секретного ключа D:
S3 = S1 * S2 (mod N).
Действительно,
S1 * S2 (mod N) = m1D * m2D (mod N) = (m1m2)D (mod N) = m3D (mod N) = S3 .
Более надежный и удобный для
реализации на персональных компьютерах алгоритм цифровой подписи был разработан
в 1984 г. американцем арабского происхождения Тахером Эль Гамалем. В 1991 г.
НИСТ США обосновал перед комиссией Конгресса США выбор алгоритма цифровой
подписи Эль Гамаля в качестве основы для национального стандарта.
Название ЕGSА происходит от слов Е_ Gаmа_ Signaturе Аlgorithm (алгоритм
цифровой подписи Эль Гамаля). Идея ЕGSА
основана на том, что для обоснования практической невозможности фальсификации
цифровой подписи может быть использована более сложная вычислительная задача,
чем разложение на множители большого целого числа,- задача дискретного
логарифмирования.
Рассмотрим подробнее алгоритм
цифровой подписи Эль-Гамаля. Для того чтобы генерировать пару ключей (открытый
ключ – секретный ключ), сначала выбирают некоторое большое простое целое число Р
и большое целое число G, причем G < Р.
Отправитель и получатель подписанного
документа используют при вычислениях одинаковые большие целые числа Р
(~10308 или ~21024) и G (~10154 или
~2512), которые не являются секретными.
Отправитель выбирает случайное целое
число X, 1 < Х £ (Р-1), и вычисляет
Y =GX mod Р .
Число Y является открытым ключом, используемым для проверки подписи
отправителя. Число Y открыто передается всем потенциальным получателям
документов.
Число Х является секретным ключом
отправителя для подписывания документов и должно храниться в секрете.
Для того чтобы подписать сообщение М, сначала отправитель хэширует его с
помощью хэш-функции h(·) в целое число m:
m = h(М), 1 < m < (Р-1) ,
и генерирует случайное целое число
К, 1 < К < (Р-1)
, такое, что
К(Р-1)
являются взаимно простыми. Затем отправитель вычисляет целое число
а
а = GK mod Р
и, применяя расширенный алгоритм
Евклида, вычисляет с помощью секретного ключа
Х
целое число
b
из уравнения
m = Х * а К * b (mod (Р-1)) .
Пара чисел (а,b) образует цифровую подпись S:
S=(а,b) ,
проставляемую под документом
М
Тройка чисел (М,а,b) передается
получателю, в то время как пара чисел (Х,К) держится в секрете.
После приема подписанного сообщения (М,а,b) получатель должен проверить,
соответствует ли подпись S=(а,b) сообщению М. Для этого
получатель сначала вычисляет по принятому сообщению М число
m = h(М) ,
т.е. хэширует принятое сообщение
М
Затем получатель вычисляет значение
А = Ya ab (mod Р)
и признает сообщение
М
подлинным, только если
А = Gm (mod Р) .
Иначе говоря, получатель проверяет справедливость соотношения
Ya ab (mod Р) = Gm (mod Р) .
Можно строго математически доказать,
что последнее равенство будет выполняться тогда, и только тогда, когда подпись
S=(а,b) под документом М получена с помощью именно того
секретного ключа X, из которого был получен открытый ключ Y.
Таким образом,
можно надежно удостовериться, что отправителем сообщения М был обладатель
именно данного секретного ключа X, не раскрывая при этом сам ключ, и что
отправитель подписал именно этот конкретный документ М.
Следует отметить, что выполнение
каждой подписи по методу Эль Гамаля требует нового значения К, причем это
значение должно выбираться случайным образом. Если нарушитель раскроет
когда-либо значение К, повторно используемое отправителем, то он сможет раскрыть
секретный ключ Х отправителя.
Пример. Выберем: числа Р = 11, G = 2 и
секретный ключ Х = 8. Вычисляем значение открытого ключа:
Y = GX mod Р = 28 mod 11 = 3 .
Предположим, что исходное
сообщение М характеризуется хэш-значением m = 5.
Для того чтобы вычислить цифровую
подпись для сообщения М, имеющего хэш-значение m = 5, сначала выберем случайное
целое число К = 9. Убедимся, что числа К и (Р-1) являются взаимно простыми.
Действительно, НОД (9,10) = 1. Далее вычисляем элементы а и b подписи:
а = GK mod Р = 29 mod 11 = 6 ,
элемент
b
определяем, используя расширенный алгоритм Евклида:
m = Х * а К * b (mod(Р-1)).
При m = 5, а = 6, Х = 8, К = 9, Р = 11 получаем
5 = 8 * 6 9 * b (mod 10)
или
9 * b = -43 (mod 10) .
Решение: b = 3. Цифровая подпись
представляет собой пару: а = 6, b = 3. Далее отправитель передает подписанное
сообщение. Приняв подписанное сообщение и открытый ключ Y = 3, получатель
вычисляет хэш-значение для сообщения М : m = 5, а затем вычисляет два числа:
Yaab (mod Р) = 36 * 63 (mod 11) = 10 (mod 11); Gm (mod Р) = 25 (mod 11) = 10 (mod 11).
Так как эти два целых числа равны,
принятое получателем сообщение признается подлинным.
Следует отметить, что схема Эль Гамаля является характерным примером
подхода, который допускает пересылку сообщения М в открытой форме вместе с
присоединенным аутентификатором (а,b). В таких случаях процедура установления
подлинности принятого сообщения состоит в проверке соответствия аутентификатора сообщению.
Схема цифровой подписи Эль Гамаля имеет ряд преимуществ по сравнению со схемой цифровой
подписи RSА:
- При заданном уровне стойкости
алгоритма цифровой подписи целые числа, участвующие в вычислениях, имеют запись
на 25% короче, что уменьшает сложность вычислений почти в два раза и позволяет
заметно сократить объем используемой памяти. - При выборе модуля Р достаточно
проверить, что это число является простым и что у числа (Р-1) имеется большой
простой множитель (т.е. всего два достаточно просто проверяемых
условия). - Процедура формирования подписи по схеме Эль Гамаля не позволяет вычислять
цифровые подписи под новыми сообщениями без знания секретного ключа (как в RSА).
Однако алгоритм цифровой подписи Эль Гамаля имеет и некоторые недостатки по
сравнению со схемой подписи RSА. В частности, длина цифровой подписи получается
в 1,5 раза больше, что, в свою очередь, увеличивает время ее вычисления.
Первый учебный алгоритм хеширования
Входом для данного алгоритма является строка, состоящая из букв русского языка.
Выбирается число
 – вектор инициализации. Число
– вектор инициализации. Число  равно длине сообщения в символах.
равно длине сообщения в символах.Для каждого символа сообщения вычисляется значение
 , где
, где 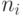 – номер
– номер  -й буквы сообщения в алфавите. Для удобства вычислений ниже приведен нумерованный алфавит.
-й буквы сообщения в алфавите. Для удобства вычислений ниже приведен нумерованный алфавит.- Значение
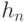 , вычисленное для последнего символа, является хеш-значением сообщения:
, вычисленное для последнего символа, является хеш-значением сообщения: 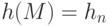 .
.
Следует отметить, что вычисленное по этому алгоритму хеш-значение зависит от всех символов сообщения 
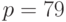
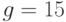


 Пример 9.2Выполнить вычисление и проверку подписи сообщения
Пример 9.2Выполнить вычисление и проверку подписи сообщения  по алгоритму Эль-Гамаля. Использовать параметры подписи:
по алгоритму Эль-Гамаля. Использовать параметры подписи:
- Сформируем хэш-сумму сообщения. Начальное значение
 равно количеству символов сообщения:
равно количеству символов сообщения:  . Далее,
. Далее, - Вычисляем число
 по формуле
по формуле 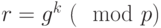 . Для рассматриваемого примера получили:
. Для рассматриваемого примера получили: - Вычисляем число
 по формуле
по формуле  , для рассматриваемого примера
, для рассматриваемого примера - Вычисляем значение
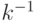 по модулю
по модулю  с помощью расширенного алгоритма Евклида. Для рассматриваемого примера значение
с помощью расширенного алгоритма Евклида. Для рассматриваемого примера значение  .
.Примечание: если полученное значение
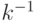 – отрицательное, следует взять его по модулю
– отрицательное, следует взять его по модулю  .
. - Вычисляем число
 по формуле
по формуле 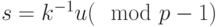 . В примере
. В примере - Цифровая подпись сообщения для рассматриваемого примера:
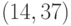 .
.
Для проверки правильности вычисления полученной цифровой подписи следует произвести ее проверку с помощью открытого ключа абонента и убедиться, что подпись подлинная.
- Сформируем открытый ключ
 абонента по формуле
абонента по формуле 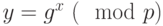 :
:Для рассматриваемого примера
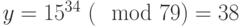 .
. Аналогичным образом вычисляем значения
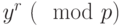 и
и  , а затем их произведение по модулю
, а затем их произведение по модулю  .
.В примере получаем:
- Вычисляем значение
 , значение
, значение  было получено ранее.
было получено ранее.В примере
 .
. - Проверяем выполнение равенства
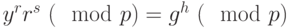 , если равенство выполняется – подпись подлинная, то есть она была вычислена правильно.
, если равенство выполняется – подпись подлинная, то есть она была вычислена правильно.В примере получили
 , равенство выполняется, значит, подпись сгенерирована правильно.
, равенство выполняется, значит, подпись сгенерирована правильно.
Проверка подписи
Входные данные: сообщение 

Выходные данные: заключение о подлинности или фальсификации подписи.
Алгоритм:
- Если хотя бы одно из условий
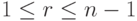 ,
,  нарушается, то подпись фальшивая и работа алгоритма закончена.
нарушается, то подпись фальшивая и работа алгоритма закончена. - Вычислить
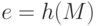 .
. - Вычислить
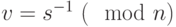 .
. - Вычислить
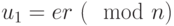 .
. - Вычислить
 .
. - Вычислить
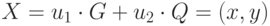 .
. - Если
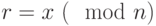 , то подпись действительная, иначе подпись фальшивая.
, то подпись действительная, иначе подпись фальшивая.
Доказательство корректности алгоритма генерации и алгоритма проверки подписи очень простое и предоставляется в качестве упражнения.
Пример 9.5Требуется проверить подлинность подписи (11,9) для сообщения  , хэш-образ которого
, хэш-образ которого 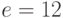 .Секретный ключ нам неизвестен, открытый ключ абонента, подписавшего сообщение, равен
.Секретный ключ нам неизвестен, открытый ключ абонента, подписавшего сообщение, равен 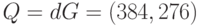 .Проверка подписи начинается с проверки условий
.Проверка подписи начинается с проверки условий 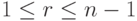
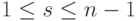
Находим точку
Наконец, сравниваем значения 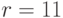

Приведем пример системы электронной подписи на эллиптической кривой, пригодный для практического применения.
Пример 9.6Рассмотрим эллиптическую кривую
Её порядок
является простым числом, а порождающим элементом группы является точка
Для построения электронной подписи нужно выбрать закрытый ключ 
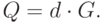
Система цифровой подписи построена.
Если читатель не имеет инструмента для работы с кривыми таких размеров, предлагаем небольшую программу на языке с , вызывающую функцию библиотеки cryptopp для перемножение точек:
Для её сборки нужно подключить библиотеку cryptopp (см. параграф 1.16.2). Допустим, мы собрали программу в исполняемый файл mulpoint (или mulpoint.exe под Windows).
Программа запускается из командной строки:
и выводит результат через стандартный выходной поток. Например:
(здесь $ – приглашение командной строки linux). В нашем случае, помимо 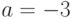
Функция перестановок
Базовая функция перестановки состоит из
Шаг
Шаг
Шаг
Шаг
Шаг
Тета, Ро, Пи, Хи, Йота
Далее будем использовать следующие обозначения:
Так как состояние
Я хочу вкратце описать каждый шаг функции перестановок, не вдаваясь в математические свойства каждого.
Шаг Эффект отображения
Схематическое представление функции:
Псевдокод шага:
Шаг
Проще всего его описать псевдокодом и схематическим рисунком:
ШагШаг
Псевдокод и схематическое представление:
Шаг Отображение
Все шаги можно объединить вместе и тогда мы получим следующее:
Где константы






2.jpg)
